题目内容
已知函数f(x)的定义域为D,如果存在实数M,使对任意的x∈D,都有|f(x)|≤M,则称函数f(x)为有界函数,下列函数:
①f(x)=2-|x|,x∈R ②f(x)=ln|x|,x∈(0,+∞)
③f(x)=
,x∈(-∞,0)∪(0,+∞) ④f(x)=xsinx,x∈(0,+∞)
为有界函数的是( )
①f(x)=2-|x|,x∈R ②f(x)=ln|x|,x∈(0,+∞)
③f(x)=
| x |
| x2+1 |
为有界函数的是( )
| A、②④ | B、②③④ |
| C、①③ | D、①③④ |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:由题意,首先理解有界函数的定义,再对4个函数依次判断即可.
解答:
解:①|f(x)|=2-|x|≤20=1,故是有界函数;
②当x→0时,|f(x)|=|lnx|→+∞,x∈(0,+∞),故不是有界函数;
③|f(x)|=|
|=
≤
,x∈(-∞,0)∪(0,+∞),故是有界函数;
④当x=2kπ+
,k∈Z时,f(x)=2kπ+
,当k→+∞时,2kπ+
→+∞,故不是有界函数;
故选C.
②当x→0时,|f(x)|=|lnx|→+∞,x∈(0,+∞),故不是有界函数;
③|f(x)|=|
| x |
| x2+1 |
| 1 | ||
|x|+
|
| 1 |
| 2 |
④当x=2kπ+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选C.
点评:本题考查了学生对新定义的接受能力及应用,属于中档题.

练习册系列答案
相关题目
若x>y>0,是
<
的( )
| 1 |
| x |
| 1 |
| y |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知f(x)是周期为4的奇函数,f(3)=2,则f(9)=( )
| A、6 | B、-6 | C、2 | D、-2 |
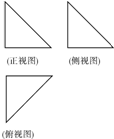 已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )A、6+2
| ||
B、6+4
| ||
C、12+4
| ||
D、8+4
|
已知集合A={x|mx2-mx+1=0}只有一个真子集,则实数m的值为( )
| A、0 | B、4 | C、0或4 | D、0或-4 |