题目内容
9.函数y=$\sqrt{sin(\frac{π}{3}-2x)}$的单调增区间是( )| A. | [k$π-\frac{π}{12}$,k$π+\frac{π}{6}$],k∈Z | B. | [k$π-\frac{π}{3}$,k$π-\frac{π}{12}$],k∈Z | ||
| C. | [k$π-\frac{π}{12}$,k$π+\frac{5π}{12}$],k∈Z | D. | [k$π+\frac{5π}{12}$,k$π+\frac{11π}{12}$],k∈Z |
分析 先求出函数y的定义域,再求函数y的单调递增区间是什么.
解答 解:∵函数y=$\sqrt{sin(\frac{π}{3}-2x)}$,
∴sin($\frac{π}{3}$-2x)≥0,
即sin(2x-$\frac{π}{3}$)≤0,
解得-π+2kπ≤2x-$\frac{π}{3}$≤2kπ,k∈Z,
即-$\frac{2π}{3}$+2kπ≤2x≤$\frac{π}{3}$+2kπ,k∈Z,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
即y的定义域是[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z;
又令$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,k∈Z,
即$\frac{5π}{6}$+2kπ≤2x≤$\frac{11π}{6}$+2kπ,k∈Z,
解得$\frac{5π}{12}$+kπ≤x≤$\frac{11π}{12}$+kπ,k∈Z,
即-$\frac{7π}{12}$+kπ≤x≤-$\frac{π}{12}$+kπ,k∈Z;
综上,函数y的单调递增区间是[-$\frac{π}{3}$+kπ,-$\frac{π}{12}$+kπ],k∈Z.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了复合函数的单调性问题,是基础题目.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.已知点P(x,y)的坐标满足$\left\{\begin{array}{l}{x+y-4≤0}\\{1≤x≤2}\\{y≥0}\end{array}\right.$则z=x+2y的最大值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.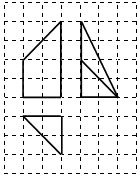 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.已知各项均为正数的等比数列{an}中,a5•a6=4,则数列{log2an}的前10项和为( )
| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
18.某中学共8个艺术社团,现从中选10名同学组成新春社团慰问小组,其中书法社团需选出3名同学,其他各社团各选出1名同学,现从这10名同学中随机选取3名同学,到社区养老院参加“新春送欢乐”活动(每位同学被选到的可能性相同),则选出的3名同学来自不同社团的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{7}{24}$ | C. | $\frac{49}{60}$ | D. | $\frac{1}{10}$ |