题目内容
20.函数f(x)=sin2x•cos(α-$\frac{π}{4}$)+(1-2sin2x)•sin(α-$\frac{π}{4}$).(1)若α∈[$\frac{π}{4}$,$\frac{π}{2}$],x∈[0,$\frac{π}{2}$],求f(x)的最大值;
(2)是否存在实数x与α,使得f(x)=2-cosα成立?若存在,请给出一组,若不存在,说明理由.
分析 (1)化简可得f(x)=sin(2x+α-$\frac{π}{4}$),由角的范围可得最值;
(2)当x=$\frac{3π}{8}$且α=0时,满足题意.
解答 解:(1)化简可得f(x)=sin2x•cos(α-$\frac{π}{4}$)+(1-2sin2x)•sin(α-$\frac{π}{4}$)
=sin2x•cos(α-$\frac{π}{4}$)+cos2x•sin(α-$\frac{π}{4}$)=sin(2x+α-$\frac{π}{4}$),
∵α∈[$\frac{π}{4}$,$\frac{π}{2}$],x∈[0,$\frac{π}{2}$],∴2x+α-$\frac{π}{4}$∈[0,$\frac{5π}{4}$],
∴当2x+α-$\frac{π}{4}$=$\frac{π}{2}$时,f(x)取最大值1;
(2)当x=$\frac{3π}{8}$且α=0时,f(x)=f($\frac{3π}{8}$)=sin($\frac{3π}{4}$+0-$\frac{π}{4}$)=1,
此时2-cosα=2-cos0=2-1=1,满足f(x)=2-cosα成立.
点评 本题考查三角函数的恒等变换,涉及三角函数的最值,属基础题.

练习册系列答案
相关题目
10.求下列函数的零点,可以采用二分法的是( )
| A. | f(x)=x4 | B. | f(x)=tanx+2(-$\frac{π}{2}$<x<$\frac{π}{2}$) | ||
| C. | f(x)=cosx-1 | D. | f(x)=|2x-3| |
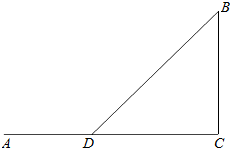 如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.
如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.