题目内容
四面体的顶点和各棱中点共10个点,任取4个点不共面的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式,棱锥的结构特征
专题:计算题,分类讨论
分析:先利用组合求出10个点中取4个点的所有的基本事件个数;利用分类讨论的方法求出取出的四点在一个平面上的所有的基本事件个数;利用对立事件求出不共面的所有的基本的事件个数;利用古典概型概率公式求出这四个点不共面的概率.
解答:
 解:10个点中取4个点的取法为C104=210种,
解:10个点中取4个点的取法为C104=210种,
其中共面的分三种情况:
①、四个点都在四面体的某一个面上,每个面6个点,有 C64=15种,四个面共有4×15=60种情况.
②、其中三点共线,另一个点与此三点不在四面体的某一个面上,而在与此三点所在直线异面的那条直线的中点,
显然只有6种情况(因为四面体只有6条边).
③、其中两点所在直线与另两点所在直线平行,且这四个点也不在四面体的某一个面上,画图可得出只有3种情况.
∴取四个不共面的点的不同取法共有:210-60-6-3=141种,
∴这四个点不共面的概率为
=
.
故选:B.
 解:10个点中取4个点的取法为C104=210种,
解:10个点中取4个点的取法为C104=210种,其中共面的分三种情况:
①、四个点都在四面体的某一个面上,每个面6个点,有 C64=15种,四个面共有4×15=60种情况.
②、其中三点共线,另一个点与此三点不在四面体的某一个面上,而在与此三点所在直线异面的那条直线的中点,
显然只有6种情况(因为四面体只有6条边).
③、其中两点所在直线与另两点所在直线平行,且这四个点也不在四面体的某一个面上,画图可得出只有3种情况.
∴取四个不共面的点的不同取法共有:210-60-6-3=141种,
∴这四个点不共面的概率为
| 141 |
| 210 |
| 47 |
| 70 |
故选:B.
点评:本题考查利用排列、组合求完成事件的方法数、考查分类讨论的数学思想方法、考查对立事件的概率的求法.

练习册系列答案
相关题目
已知直线ax+2y+1=0与直线4x+6y+11=0垂直,则a的值是( )
| A、-5 | B、-1 | C、-3 | D、1 |
在矩形ABCD中,AB=2,AD=5,如果在该矩形内随机找一点P,那么使得△ABP与△CDP的面积都不小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则下列图象错误的是( )
|
A、 y=f(x-1)的图象 |
B、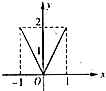 y=f(|x|)的图象 |
C、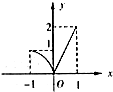 y=f(-x) 的图象 |
D、 y=f(x)的图象 |
若关于x的不等式m≤
x2-2x+3≤n的解集是[m,n](m,n∈R),则n-m的值是( )
| 2 |
| 3 |
| A、3 | ||
| B、2 | ||
C、
| ||
| D、4 |
某商品原价200元,若连续两次涨价10%后出售,则新售价为( )
| A、222元 | B、240元 |
| C、242元 | D、484元 |



