题目内容
在矩形ABCD中,AB=2,AD=5,如果在该矩形内随机找一点P,那么使得△ABP与△CDP的面积都不小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:根据题意,可得满足条件的P点位于矩形ABCD中间,长为2宽为3的一个小矩形当中,如图所示.由此结合几何概型计算公式,即可算出使△ABP与△CDP的面积都不小于1的概率.
解答:
解:由题意,以AB为底边,要使△ABP面积不小于1,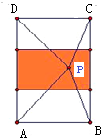
而S△ABP=
AB×h=h,即△ABP的高h≥1,
同理△CD的高h'≥1,
因此,P点到AB和CD的距离都要不小于1,相应的区域为图中阴影部分,
它的面积为S'=3×2=6
而矩形ABCD的面积为S=2×5=10
∴所求概率P=
=
故选:C.

而S△ABP=
| 1 |
| 2 |
同理△CD的高h'≥1,
因此,P点到AB和CD的距离都要不小于1,相应的区域为图中阴影部分,
它的面积为S'=3×2=6
而矩形ABCD的面积为S=2×5=10
∴所求概率P=
| S′ |
| S |
| 3 |
| 5 |
故选:C.
点评:本题给出几何概型,在矩形ABCD中求使得△ABP与△CDP的面积都不小于1的概率.着重考查了矩形、三角形的面积公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
相关题目
已知f(x)是定义域为实数集R的偶函数,?x1≥0,?x2≥0,若x1≠x2,则
<0.如果f(
)=
,4f(log
x)>3,那么x的取值范围为( )
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 8 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
已知复数z=
,则复数z在复平面内对应的点位于( )
| 1+i+i2+i3+…+i 2014 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
四面体的顶点和各棱中点共10个点,任取4个点不共面的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=i,
是z的共轭复数,则
=( )
. |
| z |
| ||
| z |
| A、1 | B、-i | C、i | D、-1 |
函数f(x)=lg丨x+1丨的图象大致是( )
A、 |
B、 |
C、 |
D、 |
函数y=
的图象大致是( )
| lg|x| |
| x |
A、 |
B、 |
C、 |
D、 |