题目内容
4．如果两条直线l1：ax+2y+6=0与l2：x+（a-1）y+3=0平行，那么实数a等于（ ）| A． | -1 | B． | 2 | C． | 2或-1 | D． | $\frac{2}{3}$ |
分析 两条直线l1：ax+2y+6=0与l2：x+（a-1）y+3=0平行，直线l1的斜率存在，利用两条直线相互平行的充要条件即可得出．
解答 解：∵两条直线l1：ax+2y+6=0与l2：x+（a-1）y+3=0平行，直线l1的斜率存在，
分别化为：y=-$\frac{a}{2}$x-3，y=$\frac{-1}{a-1}x$-$\frac{3}{a-1}$，
∴$-\frac{a}{2}=-\frac{1}{a-1}$，-3≠-$\frac{3}{a-1}$，
解得a=-1．
故选：A．
点评 本题考查了两条直线相互平行的充要条件，考查了推理能力与计算能力，属于中档题．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
14．有下列四个命题：
①若xy＞0，则x，y同正或同负；
②周长相等的两个三角形全等；
③若m≤0，则x2-2x+m=0有实数解；
④若A∪B=B，则A⊆B．
其中真命题个数为（ ）
①若xy＞0，则x，y同正或同负；
②周长相等的两个三角形全等；
③若m≤0，则x2-2x+m=0有实数解；
④若A∪B=B，则A⊆B．
其中真命题个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
16．方程ex-x-2=0的一个根所在的区间（k，k+1）（k∈N），则k的值为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
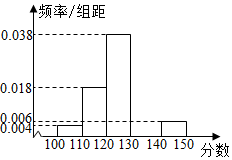2015-2016学年高二A班50名学生在其中数学测试中（满分150分），成绩都介于100分到150分之间，将测试结果按如下方式分成五组，第一组[100，110），第二组[110，120），…，第五组[140，150），按上述分组方法得到的频率分布直方图如图所示，