题目内容
14.有下列四个命题:①若xy>0,则x,y同正或同负;
②周长相等的两个三角形全等;
③若m≤0,则x2-2x+m=0有实数解;
④若A∪B=B,则A⊆B.
其中真命题个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①由xy>0判断即可;
②根据全等的定义判断;
③根据一元二次方程根的判断;
④集合交集,并集的概念判断.
解答 解:①若xy>0,则x,y同正或同负,即同号,故正确;
②周长相等的两个三角形全等,显然错误;
③若m≤0,△=4-4m>0,则x2-2x+m=0有实数解,故正确;
④若A∪B=B,则A⊆A∪B=B,故正确.
故选:C.
点评 考查了三角形全等,一元二次方程根的判断,集合的交集,并集.属于基础题型,应熟练掌握.

练习册系列答案
相关题目
19.已知0<a<1,f(x)=ax,g(x)=logax,h(x)=$\sqrt{x}$,当x>1时,则有( )
| A. | f(x)<g(x)<h(x) | B. | g(x)<f(x)<h(x) | C. | g(x)<h(x)<f(x) | D. | h(x)<g(x)<f(x) |
4.如果两条直线l1:ax+2y+6=0与l2:x+(a-1)y+3=0平行,那么实数a等于( )
| A. | -1 | B. | 2 | C. | 2或-1 | D. | $\frac{2}{3}$ |
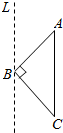 如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.
如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.