题目内容
16．已知{an}是公差为2的等差数列，前5项和S5=25，若a2m=15，则m=（ ）| A． | 4 | B． | 6 | C． | 7 | D． | 8 |
分析 利用等差数列通项公式求出首项，从而求出通项公式，由此利用a2m=15，能求出m的值．
解答 解：∵{an}是公差为2的等差数列，前5项和S5=25，
∴${S}_{5}=5{a}_{1}+\frac{5×4}{2}d$=$5{a}_{1}+\frac{5×4}{2}×2$=25，
解得a1=1，
∴an=1+（n-1）×2=2n-1，
∵a2m=15，
∴a2m=2（2m）-1=15，
解得m=4．
故选：A．
点评 本题考查等差数列的项数的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
1．
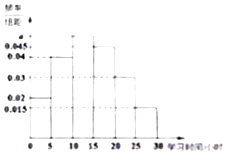某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间不少于15小时的人数是（ ）
某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间不少于15小时的人数是（ ）| A． | 27 | B． | 33 | C． | 135 | D． | 165 |
8．将函数f（x）=sin（2x+θ）（-$\frac{π}{2}$＜θ＜$\frac{π}{2}$）的图象向右平移φ（0＜φ＜π）个单位长度后得到函数g（x）的图象，若f（x），g（x）的图象都经过点P（0，$\frac{\sqrt{3}}{2}$），则φ的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2}{3}$π | D． | $\frac{5}{6}$π |
5．设Sn是等差数列{an}的前n项和，且a3=S3=3，则a4+a5=（ ）
| A． | 12 | B． | 9 | C． | 6 | D． | 3 |