题目内容
4.数列{an}的前n项和Sn满足:Sn=n2,数列{bn}满足:①b3=$\frac{1}{4}$,②bn>0,③bn+12+bn+1bn-bn2=0.(1)求数列{an}与{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
分析 (1)数列{an}的前n项和Sn满足:Sn=n2,可得n=1时,a1=S1=1;n≥2时,an=Sn-Sn-1.数列{bn}满足:①b3=$\frac{1}{4}$,②bn>0,③bn+12+bn+1bn-bn2=0.变形$(\frac{{b}_{n+1}}{{b}_{n}})^{2}$+$\frac{{b}_{n+1}}{{b}_{n}}$-1=0,解得$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{\sqrt{5}-1}{2}$.利用等比数列的通项公式即可得出.
(2)cn=anbn=(2n-1)×$\frac{1}{4}×(\frac{\sqrt{5}-1}{2})^{n-3}$,令q=$\frac{\sqrt{5}-1}{2}$.cn=$\frac{1}{4}•(2n-1)•{q}^{n-3}$.利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)∵数列{an}的前n项和Sn满足:Sn=n2,∴n=1时,a1=S1=1;n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
n=1时也成立,∴an=2n-1.
∵数列{bn}满足:①b3=$\frac{1}{4}$,②bn>0,③bn+12+bn+1bn-bn2=0.
∴$(\frac{{b}_{n+1}}{{b}_{n}})^{2}$+$\frac{{b}_{n+1}}{{b}_{n}}$-1=0,解得$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{\sqrt{5}-1}{2}$.
∴数列{bn}是等比数列,bn=$\frac{1}{4}×(\frac{\sqrt{5}-1}{2})^{n-3}$.
(2)cn=anbn=(2n-1)×$\frac{1}{4}×(\frac{\sqrt{5}-1}{2})^{n-3}$,令q=$\frac{\sqrt{5}-1}{2}$.
cn=$\frac{1}{4}•(2n-1)•{q}^{n-3}$.
数列{cn}的前n项和Tn=$\frac{1}{4}$[q-2+3•q-1+5+…+(2n-1)•qn-3].
qTn=$\frac{1}{4}$[q-1+3+5q+…+(2n-3)•qn-3+(2n-1)qn-2],
∴(1-q)Tn=$\frac{1}{4}$[q-2+2(q-1+1+q+…+qn-3)-(2n-1)qn-2]=$\frac{1}{4}[{q}^{-2}+2×\frac{\frac{1}{q}(1-{q}^{n-1})}{1-q}-(2n-1){q}^{n-2}]$,
∴Tn=$\frac{{q}^{-2}}{4(1-q)}$+$\frac{1-{q}^{n-2}}{q(1-q)^{2}}$-$\frac{(2n-1){q}^{n-2}}{1-q}$.其中q=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了等比数列的通项公式与求和公式、“错位相减法”、数列递推关系,考查了推理能力与计算能力,属于中档题.

| A. | x=2 | B. | x=-2 | C. | y=2 | D. | y=-2 |
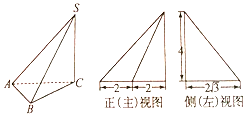
| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $16\sqrt{3}$ |
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
| A. | ?x∈Z,x2+2x-1≥0 | B. | ?x∈Z,使x2+2x-1>0 | ||
| C. | ?x∈Z,x2+2x+1>0 | D. | ?x∈Z,使x2+2x-1≥0 |
