题目内容
9．三棱锥P-ABC三条侧棱两两垂直，三条侧棱长分别为$1，\sqrt{5}，\sqrt{10}$，求该三棱锥的外接球体积．分析 由题意画出图形，把三棱锥补形为正方体，求出正方体的体对角线长，得到三棱锥的外接球的半径，则答案可求．
解答 解：如图，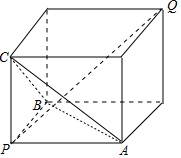
∵三棱锥P-ABC三条侧棱两两垂直，且三条侧棱长分别为$1，\sqrt{5}，\sqrt{10}$，
∴把三棱锥P-ABC补形为正方体PQ，则PQ2=${1}^{2}+（\sqrt{5}）^{2}+（\sqrt{10}）^{2}=16$，
∴PQ=4，则三棱锥的外接球的半径为$\frac{1}{2}PQ=2$．
∴三棱锥的外接球体积V=$\frac{4}{3}π×{2}^{3}$=$\frac{32}{3}π$．
点评 本题考查棱柱、棱锥、棱台的体积，补形是关键，是中档题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
20．已知等比数列{an}的公比q为正数，且a3•a7=4a42，则q=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
17．已知点A（-1，2）和点B（4，-6）在直线2x-ky+4=0的两侧，则实数k的取值范围是（ ）
| A． | （-2，1） | B． | （-1，2） | C． | （-∞，1）∪（-2，+∞） | D． | （-∞，-2）∪（1，+∞） |
4．在△ABC中，∠A=45°，a=2，b=$\sqrt{2}$，则∠B=（ ）
| A． | 30° | B． | 30°或150° | C． | 60° | D． | 60°或120° |
14．等差数列{an}和{bn}，{bn}的前n项和分别为Sn与Tn，对一切自然数n，都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{n+1}$，则$\frac{{a}_{5}}{{b}_{5}}$等于（ ）?
| A． | $\frac{3}{4}$ | B． | $\frac{5}{6}$ | C． | $\frac{9}{10}$ | D． | $\frac{10}{11}$ |