题目内容
10.已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点.(1)若$\overrightarrow{AF}$=3$\overrightarrow{FB}$,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
分析 (1)由题意可知:设直线AB的方程为:x=my+1,代入抛物线方程,由韦达定理可知:y1+y2=4m,y1•y2=-4,则$\overrightarrow{AF}$=(1-x1,-y1),$\overrightarrow{FB}$=(x2-1,y2),由$\overrightarrow{AF}$=3$\overrightarrow{FB}$,-y1=3y2,解得:m=±$\frac{\sqrt{3}}{3}$,即可求得直线AB的斜率;
(2)由(1)可知:丨y1-y2丨=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{16{m}^{2}+16}$=4$\sqrt{{m}^{2}+1}$,则四边形OACB面积SOACB=2SAOB=$\frac{1}{2}$•丨OF丨•丨y1-y2丨=丨y1-y2丨,即可求得4$\sqrt{{m}^{2}+1}$≥4,当m=0时,四边形OACB的面积最小,最小值为4.
解答 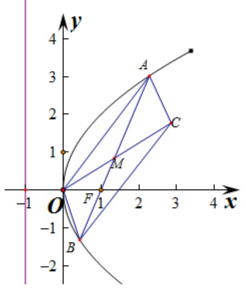 解:(1)由抛物线y2=4x的焦点在x轴上,焦点坐标F(1,0),
解:(1)由抛物线y2=4x的焦点在x轴上,焦点坐标F(1,0),
设直线AB的方程为:x=my+1,
则$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$,整理得:y2-4my-4=0,
设A(x1,y1),B(x2,y2),
由韦达定理可知:y1+y2=4m,y1•y2=-4,
$\overrightarrow{AF}$=(1-x1,-y1),$\overrightarrow{FB}$=(x2-1,y2),
∵$\overrightarrow{AF}$=3$\overrightarrow{FB}$,
∴-y1=3y2,整理得:m2=$\frac{1}{3}$,解得:m=±$\frac{\sqrt{3}}{3}$,
∴直线AB的斜率k=$\frac{1}{m}$=±$\sqrt{3}$,
直线AB的斜率$\sqrt{3}$或-$\sqrt{3}$;
(2)由(1)可知:丨y1-y2丨=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{16{m}^{2}+16}$=4$\sqrt{{m}^{2}+1}$,
四边形OACB面积SOACB=2SAOB=$\frac{1}{2}$•丨OF丨•丨y1-y2丨=丨y1-y2丨=4$\sqrt{{m}^{2}+1}$≥4,
当m=0时,四边形OACB的面积最小,最小值为4.
点评 本题考查直线与抛物线的位置关系,考查韦达定理及向量的坐标坐标,三角形面积公式的应用,考查计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案