题目内容
4.已知点P(x,y)满足不等式组$\left\{\begin{array}{l}{3x+y-7≥0}\\{x-y-1≤0}\\{x+y-5≤0}\end{array}\right.$,则z=$\frac{{x}^{2}+xy+{y}^{2}}{xy}$的范围是[3,$\frac{17}{4}$].分析 利用分式函数的性质结合换元法设t=$\frac{y}{x}$,进行转化,然后作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答 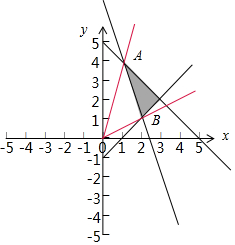 解:z=$\frac{{x}^{2}+xy+{y}^{2}}{xy}$=$\frac{x}{y}$+$\frac{y}{x}$+1,
解:z=$\frac{{x}^{2}+xy+{y}^{2}}{xy}$=$\frac{x}{y}$+$\frac{y}{x}$+1,
设t=$\frac{y}{x}$,则z=$\frac{x}{y}$+$\frac{y}{x}$+1=$\frac{1}{t}+t+1$,
作出不等式组$\left\{\begin{array}{l}{3x+y-7≥0}\\{x-y-1≤0}\\{x+y-5≤0}\end{array}\right.$,对应的平面区域如图:
则t=$\frac{y}{x}$的几何意义是区域内的点到原点的斜率,
由图象知OC的斜率最小,OB的斜率最大,
由$\left\{\begin{array}{l}{3x+y-7=0}\\{x+y-5=0}\end{array}\right.$得A(1,4),此时OA的斜率t=$\frac{4}{1}$=4,
由$\left\{\begin{array}{l}{x-y-1=0}\\{3x+y-7=0}\end{array}\right.$得B(2,1),此时OB的斜率t=$\frac{1}{2}$,
即$\frac{1}{2}$≤t≤4,
∵y=t+$\frac{1}{t}$+1在$\frac{1}{2}$≤t≤1上递减,在1≤t≤4递增,
∴当t=1时,函数取得最小值y=1+1+1=3,
当t=4或$\frac{1}{2}$时,y=4+$\frac{1}{4}$+1=$\frac{17}{4}$,y=2+$\frac{1}{2}+1$=$\frac{7}{2}$.
即3≤z≤$\frac{17}{4}$,
即z=$\frac{{x}^{2}+xy+{y}^{2}}{xy}$的取值范围是[3,$\frac{17}{4}$],
故答案为:[3,$\frac{17}{4}$].
点评 本题主要考查线性规划的应用,根据分式的性质,利用换元法进行转化结合基本不等式的性质是解决本题的关键.综合性较强,难度较大.

| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
| A. | $\frac{1}{18}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上都不对 |
| 点击量 | [0,1000] | (1000,3000] | (3000,+∞) |
| 节数 | 6 | 18 | 12 |
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<1} | D. | ∅ |
| x | 1 | 2 | 3 | 4 |
| y | m | 3.2 | 4.8 | 7.5 |
 函数f(x)=6cos2$\frac{ωx}{2}+\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与l轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}+\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与l轴的交点,且△ABC为正三角形.