题目内容
18.(1)已知点M与两个定点O(0,0)、P(2,0)的距离的比为$\sqrt{3}$:1,求点M的轨迹方程;(2)已知过点Q(-1,0)的直线l截(1)中M的轨迹的弦长为2,求直线l的方程.
分析 (1)设出M的坐标,直接由点M与两个定点O(0,0)、P(2,0)的距离的比为$\sqrt{3}$:1,列式整理得方程.
(2)过点Q(-1,0)的直线l截(1)中M的轨迹的弦长为2,可得圆心到直线的距离,利用点到直线的距离公式,建立方程,即可求直线l的方程.
解答 解:(1)设M(x,y),由点M与两个定点O(0,0)、P(2,0)的距离的比为$\sqrt{3}$:1,得
$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x-2)^{2}+{y}^{2}}}$=$\sqrt{3}$,整理得:(x-3)2+y2=3.
∴点M的轨迹方程是(x-3)2+y2=3.
(2)∵过点Q(-1,0)的直线l截(1)中M的轨迹的弦长为2,
∴圆心到直线的距离为d=$\sqrt{3-1}$=$\sqrt{2}$,
设直线l的方程为y=k(x+1),即kx-y+k=0,
∴圆心到直线的距离为$\frac{|4k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,
∴k=±$\frac{\sqrt{7}}{7}$,
∴直线l的方程为y=±$\frac{\sqrt{7}}{7}$(x+1),
点评 本题考查了轨迹方程的求法,考查了直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
10.有一个正三角形的两个顶点在抛物线y2=2px(p>0)上,另一顶点在原点,则该三角形的边长是( )
| A. | 2$\sqrt{3}$p | B. | 4$\sqrt{3}$p | C. | 6$\sqrt{3}$p | D. | 8$\sqrt{3}$p |
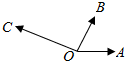 如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )
如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )