题目内容
1.已知数列{an}中${a_n}={({-1})^{\frac{{n({n+1})}}{2}}}({2n-1})$,设{an}的前n项和为Sn,则S101的值为-1.分析 先找到规律,每隔四项之和为8,即可求出答案.
解答 解:∵${a_n}={({-1})^{\frac{{n({n+1})}}{2}}}({2n-1})$,
当n=1时,a1=-1,
当n=2时,a2=-3,
当n=3时,a3=5,
当n=4时,a4=7,
当n=5时,a5=-9,
当n=6时,a6=-11,
∴S4=-1-3+5+7=8,S8-S4=-9-11+13+15=8,
每隔4项之和均为8,
101÷4=25…1
∵a101=-201.
∴S101=8×25-201=-1,
故答案为:-1
点评 本题考查了数列的递推公式和数列的前n项和,考查了学生的运算能力,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得到函数g(x)的图象如图所示,则函数f(x)的解析式是( )
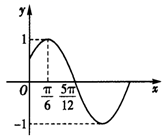

| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
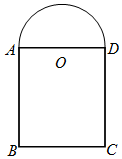 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).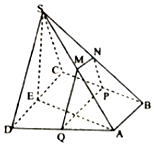 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
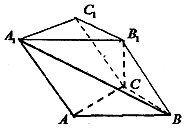 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.