题目内容
10.已知x>0,y>0,且$\frac{1}{3x+y}$+$\frac{2}{x+2y}$=2,则x+y的最小值是$\frac{9}{10}$.分析 x>0,y>0,且$\frac{1}{3x+y}$+$\frac{2}{x+2y}$=2,x+y=$\frac{1}{5}$(3x+y)+$\frac{2}{5}$(x+2y)=$\frac{1}{10}$[(3x+y)+(2x+4y)]$(\frac{1}{3x+y}+\frac{2}{x+2y})$,化简利用基本不等式的性质即可得出.
解答 解:∵x>0,y>0,且$\frac{1}{3x+y}$+$\frac{2}{x+2y}$=2,
则x+y=$\frac{1}{5}$(3x+y)+$\frac{2}{5}$(x+2y)=$\frac{1}{10}$[(3x+y)+(2x+4y)]$(\frac{1}{3x+y}+\frac{2}{x+2y})$=$\frac{1}{10}$$(5+\frac{2x+4y}{3x+y}+\frac{2(3x+y)}{x+2y})$
≥$\frac{1}{10}$$(5+2×2\sqrt{\frac{x+2y}{3x+y}×\frac{3x+y}{x+2y}})$=$\frac{9}{10}$,当且仅当y=2x=$\frac{3}{5}$时取等号.
故答案为:$\frac{9}{10}$.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2.若复数$\frac{a+3i}{1+2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | -6 | B. | 13 | C. | $\frac{3}{2}$ | D. | $\sqrt{13}$ |
12.函数f(x)=5x2+1( )
| A. | 在(0,+∞)内是增函数 | B. | 在(1,+∞)内是增函数 | ||
| C. | 在(-∞,0)内是增函数 | D. | 在(-∞,1)内是增函数 |
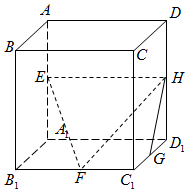 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.