题目内容
已知函数f(x)=x2+2x-a,方程f(f(x))=0有不等的4个实根,求a的取值范围.
考点:二次函数的性质,根的存在性及根的个数判断
专题:函数的性质及应用
分析:令f(x)=t,则得到f(t)=t2+2t-a=0,该方程应有两个根,所以得到a>-1,该方程的两个实根设为t1,t2,所以t1=-1+
,t2=-1-
,所以得到方程x2+2x-a=-1+
,或x2+2x-a=-1-
,这两个方程都有两个不等实根,所以根据判别式△>0即可求得a的取值范围.
| 1+a |
| 1+a |
| 1+a |
| 1+a |
解答:
解:令f(x)=t,则方程f(t)=t2+2t-a=0,有两个不等实根;
∴△=4+4a>0,a>-1;
且t1=-1+
,t2=-1-
;
∴f(x)=x2+2x-a=-1+
①,或f(x)=x2+2x-a=-1-
②;
∴(1)由①得x2+2x-a+1-
=0,则该方程有两个不等实根;
∴△=4-4(1-a-
)>0,整理得
>-a;
显然a≥0时,不等式成立;
a<0时,两边平方后得到:a2-a-1<0,解得,
<a<0;
∴a>
;
(2)同理由②可求得a>
;
∴综上得a>
;
∴a的取值范围为(
,+∞).
∴△=4+4a>0,a>-1;
且t1=-1+
| 1+a |
| 1+a |
∴f(x)=x2+2x-a=-1+
| 1+a |
| 1+a |
∴(1)由①得x2+2x-a+1-
| 1+a |
∴△=4-4(1-a-
| 1+a |
| 1+a |
显然a≥0时,不等式成立;
a<0时,两边平方后得到:a2-a-1<0,解得,
1-
| ||
| 2 |
∴a>
1-
| ||
| 2 |
(2)同理由②可求得a>
1+
| ||
| 2 |
∴综上得a>
1+
| ||
| 2 |
∴a的取值范围为(
1+
| ||
| 2 |
点评:考查一元二次方程解的情况和判别式△的关系,以及解无理不等式的方法:两边平方去根号,及解一元二次不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
(a≠0)的定义域为( )
| a2x |
| A、[0,+∞) |
| B、(0,+∞) |
| C、{0} |
| D、以上答案都不对 |
已知点P是抛物线y2=4x上一动点,则点P到点A(0,-2)的距离与到直线x=-1的距离的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
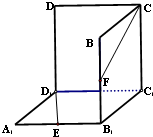 将边长为l的三个正方形面板粘合成一个空间图形,其水平放置的直观图如图所示.
将边长为l的三个正方形面板粘合成一个空间图形,其水平放置的直观图如图所示.