题目内容
8.变量x、y满足条件$\left\{\begin{array}{l}{x-y+1≤0}\\{y≤1}\\{x>-1}\end{array}\right.$,则(x-2)2+y2的最小值为5.分析 由约束条件作出可行域,利用(x-2)2+y2的几何意义,即可行域内的动点与定点M(2,0)距离的平方求得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{y≤1}\\{x>-1}\end{array}\right.$作出可行域如图,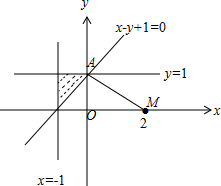
(x-2)2+y2的几何意义为可行域内的动点与定点M(2,0)距离的平方,
由图可知,(x-2)2+y2的最小值为$|MA{|}^{2}=(\sqrt{5})^{2}=5$.
故答案为:5.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.在一次射击训练中,甲、乙两名运动员各射击一次.设命题p是“甲运动员命中10环”,q是“乙运动员命中10环”,则命题“至少有一名运动员没有命中10环”可表示为( )
| A. | p∨q | B. | (¬p)∧(¬q) | C. | (¬p)∨(¬q) | D. | p∨(¬q) |
3.设{an}是等比数列,公比q=2,Sn为{an}的前n项和.记${T_n}=\frac{{17{S_n}-{S_{2n}}}}{{{a_{n+1}}}}$,n∈N*,设Tn为数列{Tn}最大项,则n=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.已知命题p:“任意的x∈R,存在m∈R,4x-2x+1-m=0且命题¬p是真命题,则实数m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<-1 | D. | m≤-1 |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别F1(-c,0),F2(c,0),若双曲线上存在点P,使得csin∠PF1F2=asin∠PF2F1,则该曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$] | B. | (1,$\sqrt{3}$] | C. | (1,$\sqrt{2}$+1] | D. | (1,$\sqrt{3}$+1] |