题目内容
19.在一次射击训练中,甲、乙两名运动员各射击一次.设命题p是“甲运动员命中10环”,q是“乙运动员命中10环”,则命题“至少有一名运动员没有命中10环”可表示为( )| A. | p∨q | B. | (¬p)∧(¬q) | C. | (¬p)∨(¬q) | D. | p∨(¬q) |
分析 先求出命题¬p和¬q,从而求出其复合命题即可.
解答 解:命题¬p:甲没射中目标,¬q:乙没射中目标;
∴“至少有一位运动员没有射中目标”就是“甲没射中目标,或乙没射中目标”;
所以可表示为(¬p)∨(¬q).
故选:C.
点评 本题考查了复合命题的表示,考查命题的否定,是一道基础题.

练习册系列答案
相关题目
7.命题“?x0∈R,使得x2=1”的否定是( )
| A. | ?x∈R,都有x2=1 | B. | ?x0∉R,使得x2=1 | C. | ?x∈R,都有x2≠1 | D. | ?x0∈R,使得x2≠1 |
11.设集合S={A0,A1,A2,A3},在S上定义运算:Ai⊕Aj=Ak,其中k为i+j被4除的余数,i,j=0,1,2,3.则满足关系式(x⊕x)⊕A2=A0的集合中的x为( )
| A. | A0与A2 | B. | A1与A2 | C. | A1与A3 | D. | A0与A3 |
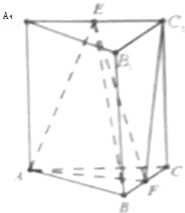 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.