题目内容
已知数列An:a1,a2,a3,…an(n∈N*,n≥2)满足a1=an=0,且当2≤k≤n(k∈N*)时,(ak-ak-1)2=1,令S(A n)=
ai.
(Ⅰ)写出的所有S(A5)可能值;
(Ⅱ)求S(An)的最大值和最小值.
| n |
 |
| i=1 |
(Ⅰ)写出的所有S(A5)可能值;
(Ⅱ)求S(An)的最大值和最小值.
考点:数列的应用
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)由题意分6种情况考虑即可;
(Ⅱ)由(ak-ak-1)2=1可构造新数列c1,c2,…,cn-2,cn-1,则它们各自的绝对值为1,和为0,则前
项取1,后
项取-1时,S(An)最大;前
项取-1,后
项取1时,S(An)最小.
(Ⅱ)由(ak-ak-1)2=1可构造新数列c1,c2,…,cn-2,cn-1,则它们各自的绝对值为1,和为0,则前
| n-1 |
| 2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
解答:
解:(Ⅰ)由题意满足条件的数列A5的所有可能情况有:
①0,1,2,1,0.此时S(A5)=4;
②0,1,0,1,0.此时S(A5)=2;
③0,1,0,-1,0.此时S(A5)=0;
④0,-1,-2,-1,0.此时S(A5)=-4;
⑤0,-1,0,1,0.此时S(A5)=0;
⑥0,-1,0,-1,0.此时S(A5)=-2,
所以S(A5)的所有可能的值为:4,2,0,-2,-4.
(Ⅱ)由(ak-ak-1)2=1,可设ak-ak-1=ck-1,
则ck-1=1或ck-1=-1(2≤k≤n(k∈N*),
因为an-an-1=cn-1,
所以an=an-1+cn-1=an-2+cn-2+cn-1=…=a1+c1+c2+…+cn-2+cn-1
因为an=a1=0,所以c1+c2+…+cn-2+cn-1=0,
所以n为奇数,c1,c2,…,cn-2,cn-1是由
个1,和
个-1构成的数列.
所以S(An)=c1+(c1+c2)+…+(c1+c2+…+cn-1)=(n-1)c1+(n-2)c2+…+2cn-2+cn-1
则当c1,c2,…,cn-2,cn-1的前
项取1,后
项取-1时,S(An)最大,
此时S(A n)max=(n-1)+(n-2)+…+
-(
+…+2+1)=
.
同理知,当c1,c2,…,cn-2,cn-1的前
项取-1,后
项取1时,
S(An)最小,此时S(A n)min=-
.
①0,1,2,1,0.此时S(A5)=4;
②0,1,0,1,0.此时S(A5)=2;
③0,1,0,-1,0.此时S(A5)=0;
④0,-1,-2,-1,0.此时S(A5)=-4;
⑤0,-1,0,1,0.此时S(A5)=0;
⑥0,-1,0,-1,0.此时S(A5)=-2,
所以S(A5)的所有可能的值为:4,2,0,-2,-4.
(Ⅱ)由(ak-ak-1)2=1,可设ak-ak-1=ck-1,
则ck-1=1或ck-1=-1(2≤k≤n(k∈N*),
因为an-an-1=cn-1,
所以an=an-1+cn-1=an-2+cn-2+cn-1=…=a1+c1+c2+…+cn-2+cn-1
因为an=a1=0,所以c1+c2+…+cn-2+cn-1=0,
所以n为奇数,c1,c2,…,cn-2,cn-1是由
| n-1 |
| 2 |
| n-1 |
| 2 |
所以S(An)=c1+(c1+c2)+…+(c1+c2+…+cn-1)=(n-1)c1+(n-2)c2+…+2cn-2+cn-1
则当c1,c2,…,cn-2,cn-1的前
| n-1 |
| 2 |
| n-1 |
| 2 |
此时S(A n)max=(n-1)+(n-2)+…+
| n+1 |
| 2 |
| n-1 |
| 2 |
| (n-1)2 |
| 4 |
同理知,当c1,c2,…,cn-2,cn-1的前
| n-1 |
| 2 |
| n-1 |
| 2 |
S(An)最小,此时S(A n)min=-
| (n-1)2 |
| 4 |
点评:本题考查数列的知识,看清题意,找出其内在规律是解决本题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| 2△x |
A、
| ||
| B、f′(x0) | ||
| C、2f′(x0) | ||
| D、-f′(x0) |
已知a=(log54)2,b=log53,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
已知正项等比数列{an}的公比为q,其前n项积为Tn,并满足a1>1,
<0,则以下结论错误的是( )
| a9a10-1 |
| a9a11-1 |
| A、0<q<1 |
| B、Tn的最大值是T10 |
| C、a9a10>1 |
| D、使Tn>1的最大自然数n为18 |
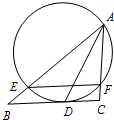 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.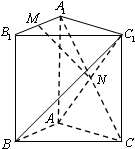 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.