题目内容
3.已知三棱锥S-ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,若该三棱锥外接球的半径为$\sqrt{3}$,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )| A. | 3 | B. | 2 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
分析 由题意,三棱锥的外接球即为以SA,SB,SC为长宽高的正方体的外接球,求出球心到平面ABC的距离,即可求出点Q到平面ABC的距离的最大值.
解答 解:∵三棱锥S-ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,
∴三棱锥的外接球即为以SA,SB,SC为长宽高的正方体的外接球,
∵该三棱锥外接球的半径为$\sqrt{3}$,
∴正方体的体对角线长为2$\sqrt{3}$,
∴球心到平面ABC的距离为$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$
∴点Q到平面ABC的距离的最大值为$\sqrt{3}$+$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
故选:D.
点评 本题考查点Q到平面ABC的距离的最大值,考查学生的计算能力,求出球心到平面ABC的距离是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
11.设函数$f(x)=\left\{\begin{array}{l}x,0≤x<1\\ \frac{1}{{f({x+1})}}-1,-1<x<0\end{array}\right.$,g(x)=f(x)-4mx-m,其中m≠0.若函数g(x)在区间(-1,1)上有且仅有一个零点,则实数m的取值范围是( )
| A. | $m≥\frac{1}{4}$或m=-1 | B. | $m≥\frac{1}{4}$ | C. | $m≥\frac{1}{5}$或m=-1 | D. | $m≥\frac{1}{5}$ |
12.已知等差数列{an}的前n项和为Sn,a9=1,S18=0,当Sn取最大值时n的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
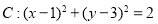 被直线
被直线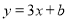 所截得的线段的长度等于2,则
所截得的线段的长度等于2,则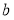 等于( )
等于( )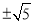 B.
B.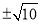 C.
C.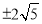 D.
D.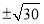
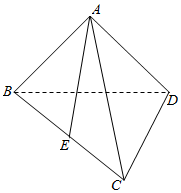 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.