题目内容
18.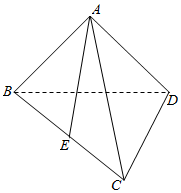 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.(Ⅰ)求证:AE⊥BD;
(Ⅱ)设平面ABD⊥平面BCD,AD=CD=2,BC=4,求三棱锥D-ABC的体积.
分析 (Ⅰ)设BD的中点为O,连接AO,EO,证明AO⊥BD,CD⊥BD,EO⊥BD.推出BD⊥平面AOE,然后证明AE⊥BD.
(Ⅱ)利用三棱锥D-ABC与C-ABD的体积相等,求出S△ABD,然后求解三棱锥C-ABD的体积即可.
解答 (Ⅰ)证明:设BD的中点为O,连接AO,EO,∵AB=AD,∴AO⊥BD,又∵E为BC的中点,∴EO∥CD,∵CD⊥BD,∴EO⊥BD.…(3分)
∵OA∩OE=O,∴BD⊥平面AOE,又∵AE?平面AOE,∴AE⊥BD.…(6分)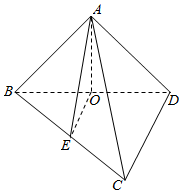
(Ⅱ)解:由已知得三棱锥D-ABC与C-ABD的体积相等.…(7分)
∵CD⊥BD,平面ABD⊥平面BCD,∴CD⊥平面ABD,BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$2\sqrt{3}$.
由已知可得:S△ABD=$\frac{1}{2}$BD•$\sqrt{A{D}^{2}-\frac{B{D}^{2}}{4}}$=$\sqrt{3}$.
∴三棱锥C-ABD的体积${V_{C-ABD}}=\frac{1}{3}×CD×{S_{△ABD}}=\frac{{2\sqrt{3}}}{3}$.
所以,三棱锥D-ABC的体积为$\frac{{2\sqrt{3}}}{3}$.…(12分)
点评 本题考查几何体的体积的求法,直线与平面垂直的性质定理的应用,考查转化思想以及计算能力,空间想象能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
3.已知三棱锥S-ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,若该三棱锥外接球的半径为$\sqrt{3}$,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )
| A. | 3 | B. | 2 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
 的顶点都在半径为
的顶点都在半径为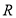 的球
的球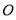 的球面上,且
的球面上,且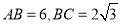 ,棱锥
,棱锥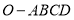 的体积为
的体积为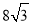 ,则
,则 如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.
如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.