题目内容
14.已知函数$f(x)=cosx•sin(x+\frac{π}{3})-\sqrt{3}{cos^2}x+\frac{{\sqrt{3}}}{4},x∈R$.(Ⅰ)求f(x)的最大值;
(Ⅱ)求f(x)的图象在y轴右侧第二个最高点的坐标.
分析 (Ⅰ)根据三角恒等变换化简f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{3}$),从而求出f(x)的最大值即可;
(Ⅱ)根据函数的表达式得到$x=kπ+\frac{5π}{12}({k∈Z})$,令k=1,得$x=\frac{17π}{12}$,从而得到满足条件的点的坐标.
解答 解:(Ⅰ)由已知,有f(x)=cos x•($\frac{1}{2}$sin x+$\frac{\sqrt{3}}{2}$cos x)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sin x•cos x-$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sin 2x-$\frac{\sqrt{3}}{4}$(1+cos 2x)+$\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sin 2x-$\frac{\sqrt{3}}{4}$cos 2x=$\frac{1}{2}$sin(2x-$\frac{π}{3}$),
所以f(x)的最大值为$\frac{1}{2}$;
(Ⅱ)令2x-$\frac{π}{3}$=$2kπ+\frac{π}{2}({k∈Z})$,
得$x=kπ+\frac{5π}{12}({k∈Z})$,
令k=1,得$x=\frac{17π}{12}$.
所以f(x) 的图象在y轴右侧第二个最高点的坐标是$({\frac{17π}{12},\frac{1}{2}})$.
点评 本题考查了三角函数的化简问题,考查三角函数的性质,是一道中档题.

练习册系列答案
相关题目
2.在区间[-1,1]上随机取一个数x,使cosπx≥$\frac{1}{2}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.已知三棱锥S-ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,若该三棱锥外接球的半径为$\sqrt{3}$,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )
| A. | 3 | B. | 2 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
4.已知等比数列{an}的前n项和为Sn,若a2=12,a3•a5=4,则下列说法正确的是( )
| A. | {an}是单调递减数列 | B. | {Sn}是单调递减数列 | ||
| C. | {a2n}是单调递减数列 | D. | {S2n}是单调递减数列 |
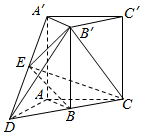 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.