题目内容
15.设(1-2x)n=a0+a1x+a2x2+…+anxn(x∈N*),若a1+a2=30,则n=5.分析 (1-2x)n=a0+a1x+a2x2+…+anxn=$1+{∁}_{n}^{1}(-2x)$+${∁}_{n}^{2}(-2x)^{2}$+…,可得a1+a2=-2+4×$\frac{n(n-1)}{2}$=30,化简解出即可得出.
解答 解:(1-2x)n=a0+a1x+a2x2+…+anxn=$1+{∁}_{n}^{1}(-2x)$+${∁}_{n}^{2}(-2x)^{2}$+…,
∴a1+a2=-2n+4×$\frac{n(n-1)}{2}$=30,化为n2-2n-15=0,n∈N*.
解得n=5.
故答案为:5.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.已知三棱锥S-ABC,满足SA⊥SB,SB⊥SC,SC⊥SA,且SA=SB=SC,若该三棱锥外接球的半径为$\sqrt{3}$,Q是外接球上一动点,则点Q到平面ABC的距离的最大值为( )
| A. | 3 | B. | 2 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
4.已知等比数列{an}的前n项和为Sn,若a2=12,a3•a5=4,则下列说法正确的是( )
| A. | {an}是单调递减数列 | B. | {Sn}是单调递减数列 | ||
| C. | {a2n}是单调递减数列 | D. | {S2n}是单调递减数列 |
5.已知P是△ABC内一点,$\overrightarrow{PB}$+$\overrightarrow{PC}$+4$\overrightarrow{PA}$=$\overrightarrow{0}$,现将一粒黄豆撒在△ABC内,则黄豆落在△PBC内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
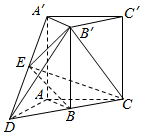 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2.
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,$AB=BC=\sqrt{2}$,A′A=2. 如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.
如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.