题目内容
函数y=log3(x-1)的定义域为( )
| A、R |
| B、(-∞,1)∪(1,∞) |
| C、(-∞,1) |
| D、(1,∞) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件,建立不等式关系即可求出函数的定义域.
解答:
解:要使函数有意义,则x-1>0,即x>1,
故函数的定义域为(1,+∞),
故选:D.
故函数的定义域为(1,+∞),
故选:D.
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
已知α是第四象限的角,并且cosα=
,那么tanα的值等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若||
|=
,|
|=2且(
-
)⊥
,则
与
的夹角是( )
| a |
| 3 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若f(x)=3sin(ωx+φ)(ω>0,|φ|<
)的周期为π且图象关于x=
对称,则( )
| π |
| 2 |
| 2π |
| 3 |
A、f(x)的图象过点(0,
| ||||
B、f(x)在[
| ||||
| C、将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象 | ||||
D、f(x)的一个对称中心是(
|
设P是△ABC内任意一点,S△ABC表示△ABC的面积,λ1=
,λ2=
,λ3=
,定义f(P)=( λ1,λ2,λ3),若G是△ABC的重心,f(Q)=(
,
,
),则( )
| S△PBC |
| S△ABC |
| S△PCA |
| S△ABC |
| S△PAB |
| S△ABC |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、点Q在△GAB内 |
| B、点Q在△GBC内 |
| C、点Q在△GCA内 |
| D、点Q与点G重合 |
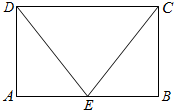 如图,矩形ABCD中,点E为边AB的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△AED或△BEC内部的概率等于( )
如图,矩形ABCD中,点E为边AB的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△AED或△BEC内部的概率等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=sinx的定义域为[a,b],值域为[-
,1],给出以下四个结论:
①b-a的最小值为
②b-a的最大值为
③a可能等于2kπ-
(k∈z)
④b可能等于2kπ-
(k∈z)
其中正确的有( )
| 1 |
| 2 |
①b-a的最小值为
| 2π |
| 3 |
②b-a的最大值为
| 4π |
| 3 |
③a可能等于2kπ-
| π |
| 6 |
④b可能等于2kπ-
| π |
| 6 |
其中正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
双曲线的两焦点坐标是F1(3,0),F2(-3,0),2b=4,则双曲线的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
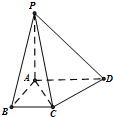 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,则PD与平面PAC所成的角大小为