题目内容
1．已知命题p：?x∈R，都有2x≥0且x2-2x≥0，则￢p为（ ）| A． | ?x∈R，都有2x≤0或x2-2x≤0 | B． | ?x0∈R，使得2x0≥0或x02-2x0≥0 | ||
| C． | ?x0∈R，使得2x0≤0且x02-2x0≤0 | D． | ?x0∈R，使得2x0＜0或x02-2x0＜0 |
分析 直接利用全称命题的否定是特称命题，写出结果即可．
解答 解：因为全称命题的否定是特称命题，
所以，命题p：?x∈R，都有2x≥0且x2-2x≥0，则￢p为：?x0∈R，使得2x0＜0或x02-2x0＜0．
故选：D．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12．
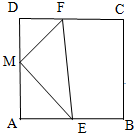如图，在正方形ABCD中，AB=2，点E、F分别在边AB、DC上，M为AD的中点，且$\overrightarrow{ME}•\overrightarrow{MF}$=0，则△MEF的面积的取值范围为（ ）
如图，在正方形ABCD中，AB=2，点E、F分别在边AB、DC上，M为AD的中点，且$\overrightarrow{ME}•\overrightarrow{MF}$=0，则△MEF的面积的取值范围为（ ）| A． | $[{1，\frac{5}{4}}]$ | B． | [1，2] | C． | $[{\frac{1}{2}，\frac{5}{4}}]$ | D． | $[{\frac{1}{2}，\frac{3}{2}}]$ |
13．已知a、b为正实数，且a+2b=3ab，若a+b-c≥0对于满足条件的a，b恒成立，则c的取值范围为（ ）
| A． | （-∞，$1+\frac{{2\sqrt{2}}}{3}$] | B． | $（-∞，\frac{3}{2}+\sqrt{2}]$ | C． | （-∞，6] | D． | （-∞，$3+2\sqrt{2}$] |
10．设y=f（t）是某港口水的深度关于时间t（时）的函数，其中0＜t≤24，下表是该港口某一天从0至24时记录的时间t与水深y的关系．
经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt-φ）的图象．根据上述数据，函数y=f（t）的解析式为（ ）
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A． | y=12+3sin$\frac{πt}{6}$，t∈[0，24] | B． | y=12+3sin（$\frac{πt}{6}$+π），t∈[0，24] | ||
| C． | y=12+3sin$\frac{πt}{12}$，t∈[0，24] | D． | y=12+3sin（$\frac{πt}{12}$+$\frac{π}{2}$），t∈[0，24] |
11．已知sin（$\frac{π}{2}$-α）=$\frac{5}{13}$，且α是第四象限的角，则tan（2π-α）=（ ）
| A． | -$\frac{12}{5}$ | B． | $\frac{12}{5}$ | C． | ±$\frac{12}{5}$ | D． | ±$\frac{5}{12}$ |