题目内容
两艘轮船都要停靠同一泊位,它们能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为1小时与2小时,求有一艘船停靠泊位时必须等待一段时间的概率为多少 .
考点:几何概型
专题:概率与统计
分析:利用几何概率公式求解.
解答:
解:以甲船到达泊位的时刻x,乙船到达泊位的时刻y分别为坐标轴,
则由题意知:0≤x,y≤24.
设事件A={有一艘轮船停靠泊位时必须等待一段时间},
事件B={甲船停靠泊位时必须等待一段时间},
事件C={乙船停靠泊位时必须等待一段时间}.
则A=B+C,并且事件B与事件C是互斥事件.
∴P(A)=P(B+C)=P(B)+P(C).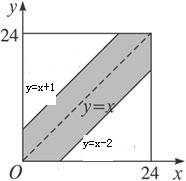
甲船停靠泊位时必须等待一段时间需满足的条件是0<x-y≤2,
乙船停靠泊位时必须等待一段时间需满足的条件是0<y-x≤1,
在如图所示的平面直角坐标系下,
点(x,y)的所有可能结果是边长为24的正方形,
事件A的可能结果由图中的阴影部分表示,
则S正方形=242=576.
S阴影=242-
(24-1)2-
(24-2)2=44.5,
∴由几何概率公式得P(A)=
=
.
∴有一艘船停靠泊位时必须等待一段时间的概率为
.
故答案为:
.
则由题意知:0≤x,y≤24.
设事件A={有一艘轮船停靠泊位时必须等待一段时间},
事件B={甲船停靠泊位时必须等待一段时间},
事件C={乙船停靠泊位时必须等待一段时间}.
则A=B+C,并且事件B与事件C是互斥事件.
∴P(A)=P(B+C)=P(B)+P(C).

甲船停靠泊位时必须等待一段时间需满足的条件是0<x-y≤2,
乙船停靠泊位时必须等待一段时间需满足的条件是0<y-x≤1,
在如图所示的平面直角坐标系下,
点(x,y)的所有可能结果是边长为24的正方形,
事件A的可能结果由图中的阴影部分表示,
则S正方形=242=576.
S阴影=242-
| 1 |
| 2 |
| 1 |
| 2 |
∴由几何概率公式得P(A)=
| 44.5 |
| 576 |
| 89 |
| 1152 |
∴有一艘船停靠泊位时必须等待一段时间的概率为
| 89 |
| 1152 |
故答案为:
| 89 |
| 1152 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意线性规划的合理运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
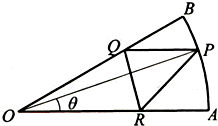 如图,已知扇形AOB是半径为2,圆心角为
如图,已知扇形AOB是半径为2,圆心角为