题目内容
设U=R，A={x|x≥1}，B={x|0＜x＜5}，则（∁UA）∩B=（ ）
| A、{x|0＜x＜1} |
| B、{x|1≤x＜5} |
| C、{x|0≤x＜1} |
| D、{x|1≤x＜5} |
考点：交、并、补集的混合运算
专题：集合
分析：根据全集U=R以及A，求出A的补集，找出A补集与B的交集即可．
解答：
解：∵U=R，A={x|x≥1}，
∴∁UA={x|x＜1}，
∵B={x|0＜x＜5}，
∴（∁UA）∩B={x|0＜x＜1}．
故选：A．
∴∁UA={x|x＜1}，
∵B={x|0＜x＜5}，
∴（∁UA）∩B={x|0＜x＜1}．
故选：A．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
若
＜
＜0，则下列不等式：（1）a+b＜ab，（2）|a|＞|b|，（3）a+c＞b+c，（4）
＜
中正确的是（ ）
| 1 |
| a |
| 1 |
| b |
| c2 |
| a |
| c2 |
| b |
| A、（1）（2） |
| B、（2）（3） |
| C、（1）（3） |
| D、（3）（4） |
已知等差数列{an}的前n项和是Sn，若S15＞0，S16＜0，则Sn最大值是（ ）
| A、S1 |
| B、S7 |
| C、S8 |
| D、S15 |
下列命题错误的是（ ）
| A、命题“若lnx=0，则x=1”的逆否命题为“若x≠1，则lnx≠0” | ||||
B、“x＞2”是“
| ||||
| C、命题p：?x∈R，使得sinx＞1，则￢p：?x∈R，均有sinx≤1 | ||||
| D、若p∧q为假命题，则p，q均为假命题 |
微积分基本定理：一般的，如果f（x）是区间[a，b]上的连续函数，并且F′（x）=f（x），那么∫
f（x）dx=（ ）
b a |
| A、F（a）-F（b） |
| B、F（b）-F（a） |
| C、F′（a）-F′（b） |
| D、F′（b）-F′（a） |
有5个不同的小球，装入4个不同的盒内，每盒至少装一个球，共有（ ）不同的装法．
| A、240 | B、120 |
| C、600 | D、360 |
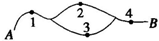如图所示，在A、B间有四个焊接点1，2，3，4，若焊接点脱落导致断路，则电路，则电路不通，今发现A、B之间电路不通，则焊点脱落的不同情况有（ ）| A、9种 | B、11种 |
| C、13种 | D、15种 |
已知角α的终边经过点P0（-3，-4），则cos（
+α）的值为（ ）
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|