题目内容
在直角坐标系xOy中，点P到两点(0，－
)、(0，)的距离之和等于4，设点P的轨迹为C，直线y＝kx＋1与C交于A、B两点．
(1)写出C的方程；
（2）若
，求k的值．
解 (1)设P(x，y)，由椭圆定义可知，点P的轨迹C是以(0，－)、(0，)为焦点，长半轴为2的椭圆，它的短半轴b＝
＝1，
故曲线C的方程为x2＋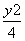
＝1.
(2)设A(x1，y1)，B(x2，y2)，
联立方程
消去y并整理得(k2＋4)x2＋2kx－3＝0.
其中Δ＝4k2＋12(k2＋4)>0恒成立．
若
，即x1x
2＋y1y2＝0.
而y1y2＝k2x1x2＋k(x1＋x2)＋1，
于是x1x2＋y1y2＝－
＋1＝0，
化简得－4k2＋1＝0，所以k＝±
.
练习册系列答案
相关题目
＋b
>a
，请选取适当的正实数a的值，分别利用所给的条件作为A、B构造命题“若A，则B”，并使得构造的原命题为真命题，而其逆命题为假命题，则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题．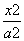
－
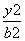＝1 (a>0，b>0)有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为________．
＋
＝1上，MP′垂直于椭圆焦点所在的直线，垂足为P′，并且M为线段PP′的中点，求P点的轨迹方程．
－y2＝1的两个焦点，点P在双曲线上，∠F1PF2＝90°，则△F1PF2的面积是________．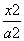
＋
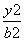＝1 (a>b>0)的焦点为F1，F2，两条准线与x轴的交点分别为M，N，若MN≤2F1F2，则该椭圆离心率的取值范围是________．
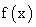在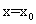
处导数存在，若p：
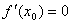；q：x=x0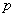是
是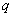
的充分必要条件
，且各次击鼓出现音乐相互独立．
．