题目内容
3.已知△ABC的面积为15$\sqrt{3}$,$\overrightarrow{BD}$+$\overrightarrow{CD}$=0,∠BAC=120°(1)求$\overrightarrow{AB}$•$\overrightarrow{AC}$的值;
(2)若AB=10,求AD的值.
分析 (1)根据三角形的面积公式可得|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=60,再根据向量的数量积公式计算即可,
(2)根据余弦定理求出BC,再根据余弦定理求出cosB,再根据余弦定理即可求出AD.
解答 解:(1)∵△ABC的面积为15$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|sin∠BAC=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=60,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos120°=60×(-$\frac{1}{2}$)=-30;
(2)∵$\overrightarrow{BD}$+$\overrightarrow{CD}$=0,
∴D为BC的中点,
∵AB=10,∴AC=6,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•AC•cosA}$=$\sqrt{100+36+60}$=14.
∴BD=$\frac{1}{2}$BC=7,
∴cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{100+196-30}{2×10×14}$=$\frac{13}{14}$,
∴AD=$\sqrt{A{B}^{2}+B{D}^{2}-2AB•BDcosB}$=$\sqrt{100+49-2×10×7×\frac{13}{14}}$=$\sqrt{19}$
点评 本题考查了向量的数量积的运算和三角形的面积公式以及余弦定理,考查了学生的运算能力,属于中档题.

| A. | 0<a<$\frac{1}{3}$ | B. | 0<a<$\frac{2}{3}$ | C. | a>$\frac{2}{3}$ | D. | $\frac{2}{3}$<a<1 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
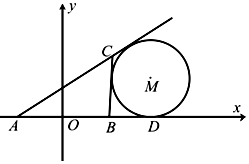 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.