题目内容

4．当1＜m＜$\frac{3}{2}$时，复数（3+i）-m（2+i）在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、几何意义、不等式的性质即可得出．

解答 解：复数（3+i）-m（2+i）=（3-2m）+（1-m）i，
∵1＜m＜$\frac{3}{2}$，∴3-2m＞0，1-m＜0，
在复平面内对应的点位于第四象限，
故选：D．

点评 本题考查了复数的运算法则、不等式的性质、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
7．函数f（x）=2sin（πx+$\frac{π}{6}$）的定义域是（-$\frac{1}{3}$，$\frac{7}{3}$]直线y=kx+1与函数f（x）的图象从左至右的交点的横坐标恰好构成等差数列，则k的值是（　　）
A．-$\frac{6}{5}$B．-1C．0D．6
15．在平面直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}x=3cosα\\ y=sinα\end{array}\right.$（α为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为$ρsin（{θ-\frac{π}{4}}）=\sqrt{2}$．
（Ⅰ）求C的普通方程和l的倾斜角；
（Ⅱ）设点P（0，2），l和C交于A，B两点，求|PA|+|PB|．
12．已知f（x）=x+xlnx，若存在实数m∈（2，+∞），使得f（m）≤k（m-2）成立，则整数k的最小取值为（　　）
A．3B．4C．5D．6
19．若（2x-1）2016=a0+a1x+…+a2016x2016（x∈R），则$\frac{1}{2}$+$\frac{{a}_{2}}{{2}^{2}{a}_{1}}$+$\frac{{a}_{3}}{{2}^{3}{a}_{1}}$+…+$\frac{{a}_{2016}}{{2}^{2016}{a}_{1}}$=（　　）
A．-$\frac{1}{2015}$B．$\frac{1}{2016}$C．-$\frac{1}{4030}$D．$\frac{1}{4032}$
9．已知集合A={x|-3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）
A．（2，6）B．（2，7）C．（-3，2]D．（-3，2）
16．若关于x的不等式xex-ax+a＜0的解集为（m，n）（n＜0），且（m，n）中只有一个整数，则实数a的取值范围是（　　）
A．[$\frac{1}{{e}^{2}}$，$\frac{1}{e}$）B．[$\frac{2}{3{e}^{2}}$，$\frac{1}{2e}$）C．[$\frac{1}{{e}^{2}}$，$\frac{2}{e}$）D．[$\frac{2}{3{e}^{2}}$，$\frac{1}{e}$）
13．已知函数f（x）为奇函数，且当x＞0时，f（x）=$\sqrt{x}$-$\frac{2}{x}$，则f（-4）=-$\frac{3}{2}$．
14．执行如图所示的程序框图，若输入的x值为2，则输出v的值为（　　）
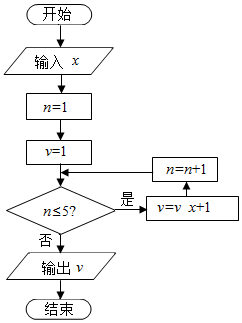
A．31B．32C．63D．64

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网