题目内容
在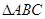 中,角
中,角 ,
,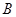 ,
,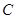 的对边为
的对边为 ,
, ,
,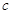 且;
且;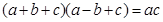
(Ⅰ)求 的值;
的值;
(Ⅱ)若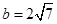 ,
,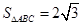 ,求
,求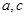 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 或者
或者
解析试题分析:(Ⅰ)因为在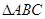 中,角
中,角 ,
,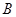 ,
,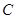 的对边为
的对边为 ,
, ,
,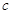 且;
且;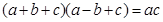 通过化简,可得三角形三边的关系,结合余弦定理即可求出结论.
通过化简,可得三角形三边的关系,结合余弦定理即可求出结论.
(Ⅱ)由三角形的面积公式即可得到一个关于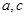 的等式,又由前题可得
的等式,又由前题可得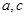 的关系式,通过解关于
的关系式,通过解关于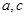 的方程即可求得结论.本题的关键就是应用三角形的余弦定理即三角形的面积公式.还有就是通过整体性解方程的思维.
的方程即可求得结论.本题的关键就是应用三角形的余弦定理即三角形的面积公式.还有就是通过整体性解方程的思维.
试题解析:(Ⅰ)由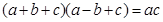 可得
可得 ,所以
,所以 .所以
.所以 . 又
. 又 ,所以
,所以 .
.
(Ⅱ)由(Ⅰ)可知 ,所以
,所以 .可得
.可得 .又由
.又由 以及余弦定理
以及余弦定理 可知
可知 ,即
,即 ,又
,又 代入可得
代入可得 .又由
.又由 可得
可得 或者
或者 .
.
考点:1.余弦定理.2.三角形的面积.3.二元二次的方程组的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,b=
,b= ,求c;
,求c; 的取值范围.
的取值范围. 为
为 ,
, 的等差中项.
的等差中项.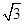 ,求b,c的值.
,求b,c的值. 中,角
中,角 所对的边分别为
所对的边分别为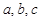 ,且
,且 ,
, ,求
,求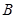 的取值范围.
的取值范围. 中,角
中,角 ,
, ,
,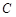 所对的边分别是
所对的边分别是 ,
,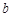 ,
,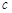 ,已知
,已知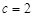 ,
,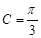 .
.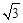 ,求
,求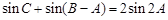 ,求
,求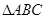 中,
中,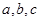 分别是内角
分别是内角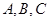 所对的边,且
所对的边,且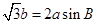 。
。 的大小;
的大小; 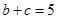 ,且
,且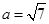 ,求
,求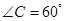 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记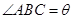 ,
,
 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?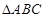 中,角
中,角 所对的边分别为
所对的边分别为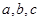 ,已知
,已知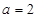 ,
,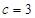 ,
,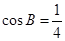 .
.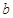 的值;
的值;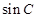 的值.
的值. ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.