题目内容
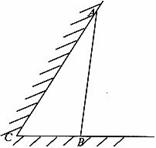
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即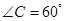 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记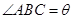 ,
,
(1)问当 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。
(1) 时,面积最大;(2)养殖场建造成扇形时面积能比(1)中的最大面积更大
时,面积最大;(2)养殖场建造成扇形时面积能比(1)中的最大面积更大
解析试题分析:(1)由余弦定理可得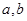 间的关系式然后用重要不等式可得
间的关系式然后用重要不等式可得 的最大值,从而求得三角形面积的最大值 也可以用正弦定理将面积用角表示出来,然后用三角函数求其最大值 (2)将扇形的面积求出来,再与(1)中的最大面积比较即可
的最大值,从而求得三角形面积的最大值 也可以用正弦定理将面积用角表示出来,然后用三角函数求其最大值 (2)将扇形的面积求出来,再与(1)中的最大面积比较即可
试题解析:(1)解法一:在 中,由余弦定理:
中,由余弦定理: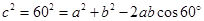 2分
2分
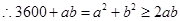 4分
4分 6分
6分

此时 8分
8分
解法二:在 中,由正弦定理:
中,由正弦定理: 2分
2分
化简得: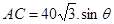 ,
,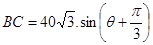 4分
4分
所以
 6分
6分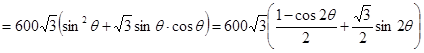
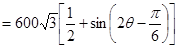
即

所以当 即
即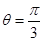 时,
时,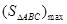
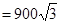 8分
8分
法若饲养场建造成扇形时,由60= 得
得
所以扇形的面积为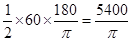 10分
10分
因为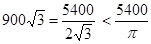
所以养殖场建造成扇形时面积能比(1)中的最大面积更大 12分
考点:1、正弦定理与余弦定理;2、三角恒等变换;3、扇形的面积;4、比较大小

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
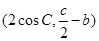 ,e2=
,e2=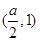 ,且e1⊥e2.
,且e1⊥e2.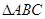 中,角
中,角 ,
,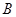 ,
,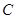 的对边为
的对边为 ,
, ,
,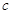 且;
且;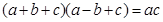
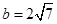 ,
,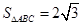 ,求
,求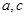 的值.
的值.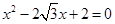 的两个根,且
的两个根,且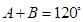 ,求△ABC的面积及AB的长.
,求△ABC的面积及AB的长.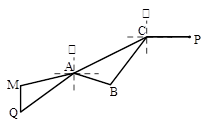
 C
C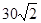 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距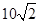 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
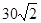 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于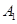 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西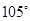 方向的
方向的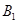 处,此时两船相距
处,此时两船相距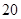 海里,当甲船航行
海里,当甲船航行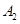 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西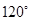 方向的
方向的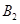 处,此时两船相距
处,此时两船相距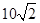 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?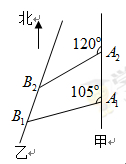
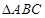 中,a,b,c分别为内角A,B,C的对边,已知:
中,a,b,c分别为内角A,B,C的对边,已知: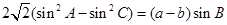 ,
,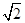 .
. 中的内角
中的内角 、
、 、
、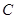 所对的边分别为
所对的边分别为 、
、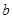 、
、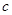 ,若
,若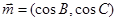 ,
,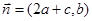 ,且
,且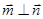 .
.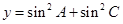 的取值范围.
的取值范围.