题目内容
设F1,F2是双曲线的两个焦点.若此双曲线上存在点P满足|PF1|=3|PF2|,则该双曲线的离心率的取值范围是 .
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:可设双曲线方程为
-
=1(a>b>0),由于双曲线上存在点P满足|PF1|=3|PF2|,则P在右支上,且|PF2|≥c-a,再由双曲线的定义,结合条件,可得|PF2|=a,再由离心率公式,即可求得范围.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:可设双曲线方程为
-
=1(a>b>0),
则F1(-c,0),F2(c,0),
由于双曲线上存在点P满足|PF1|=3|PF2|,
则P在右支上,且|PF2|≥c-a,
由双曲线的定义可知|PF1|-|PF2|=2a,
即有|PF2|=a,由a≥c-a,即有
≤2,
则1<e≤2.
则离心率的范围是(1,2].
故答案为:(1,2]
| x2 |
| a2 |
| y2 |
| b2 |
则F1(-c,0),F2(c,0),
由于双曲线上存在点P满足|PF1|=3|PF2|,
则P在右支上,且|PF2|≥c-a,
由双曲线的定义可知|PF1|-|PF2|=2a,
即有|PF2|=a,由a≥c-a,即有
| c |
| a |
则1<e≤2.
则离心率的范围是(1,2].
故答案为:(1,2]
点评:本题考查双曲线方程、定义和性质,考查离心率公式的运用和范围,考查运算能力,属于中档题.

练习册系列答案
相关题目
若x可以在|x+1|≤3的条件下任意取值,则x是负值的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设A、B为椭圆
+
=1上任意两点,O为坐标原点,则“OA⊥OB”是“O到直线AB的距离为
”的( )
| x2 |
| 16 |
| y2 |
| 9 |
| 12 |
| 5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
从装有3个红球和4个白球的口袋中任取2个小球,则下列选项中两个事件是互斥事件的为( )
| A、“都是红球”与“至少一个红球” |
| B、“恰有一个红球”与“至少一个白球” |
| C、“至少一个白球”与“至多一个红球” |
| D、“都是红球”与“至少一个白球” |
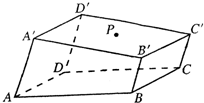 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.