题目内容
设函数f(θ)=
•
,向量
=(sinθ,cosθ),
=(sinθ,
sinθ+2cosθ),其中角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为(
,
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω
上的一个动点,试确定θ的取值范围,并求f(θ)的最小值和最大值.
| a |
| b |
| a |
| b |
| 3 |
(1)若点P的坐标为(
| 1 |
| 2 |
| ||
| 2 |
(2)若点P(x,y)为平面区域Ω
|
考点:简单线性规划,平面向量数量积的运算
专题:不等式的解法及应用
分析:(1)利用平面向量的数量积的定义和坐标公式,建立条件关系,根据三角函数的定义,即可得到结论.
(2)作出不等式组对应的平面区域,利用数形结合即可得到f(θ)的最小值和最大值.
(2)作出不等式组对应的平面区域,利用数形结合即可得到f(θ)的最小值和最大值.
解答:
 解:(1)由P(
解:(1)由P(
,
)且0≤θ≤π得θ=
;
f(θ)=
•
=sin2θ+
sinθcosθ+2cos2θ=1+cos2θ+
sin2θ=
sin2θ+
cos2θ+
=sin(2θ+
)+
,f(
)=sin(
+
)+
=2.
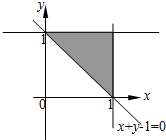
(2)如图,作出平面区域Ω
由图形可得θ∈[ 0 ,
],
f(θ)=sin(2θ+
)+
,
∵θ∈[ 0 ,
],
∴2θ+
∈[
,
]
∴f(θ)的最小值=f(
)=1;
f(θ)的最大值=f(
)=
.
 解:(1)由P(
解:(1)由P(| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
f(θ)=
| a |
| b |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| 3 |
| 2 |
(2)如图,作出平面区域Ω
由图形可得θ∈[ 0 ,
| π |
| 2 |
f(θ)=sin(2θ+
| π |
| 6 |
| 3 |
| 2 |
∵θ∈[ 0 ,
| π |
| 2 |
∴2θ+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴f(θ)的最小值=f(
| π |
| 2 |
f(θ)的最大值=f(
| π |
| 6 |
| 5 |
| 2 |
点评:本题主要三角函数的图象和性质,利用平面向量的数量积公式进行化简是解决本题的根据,注意线性规划的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题正确的是( )
| A、直线a与平面α不平行,则直线a与平面α内的所有直线都不平行 |
| B、如果两条直线在平面α内的射影平行,则这两条直线平行 |
| C、垂直于同一直线的两个平面平行 |
| D、直线a与平面α不垂直,则直线a与平面α内的所有直线都不垂直 |
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、7 |