题目内容
15．已知偶函数f（x）的定义域为R，且在（-∞，0）上是增函数，试比较$f（-\frac{3}{4}）$与f（a2-a+1）的大小．分析 利用函数奇偶性和单调性的关系进行比较大小即可．
解答 解：${a^2}-a+1={（a-\frac{1}{2}）^2}+\frac{3}{4}≥\frac{3}{4}$…（5分）
因为函数为偶函数，且在（-∞，0）上是增函数，
所以在（0，+∞）是减函数…（8分）
所以f（a2-a+1）≤$f（\frac{3}{4}）=f（-\frac{3}{4}）$…（12分）
点评 本题主要考查函数值的大小比较，利用配方法，结合函数奇偶性和单调性的性质是解决本题的关键．
练习册系列答案
相关题目
10．设函数$f（x）=\left\{\begin{array}{l}{2^{-x}}-2，x≤0\\{x^{\frac{1}{2}}}，x＞0\end{array}\right.$，如果f（x0）＞1，则x0的取值范围是（ ）
| A． | x0＜-1或x0＞1 | B． | -log23＜x0＜1 | C． | x0＜-1 | D． | x0＜-log23或x0＞1 |
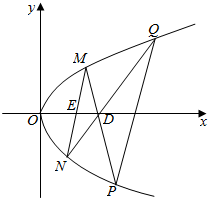如图，在平面直角坐标系中，已知抛物线C：y2=2px（p＞0）．设点D（n，0），E（m，0）．M为抛物线C上的动点（异于顶点），连接ME并延长交抛物线C于点N，连接MD、ND并延长交抛物线C于点P、Q，连接PQ．设直线MN、PQ的斜率存在且分别为k1，k2．