题目内容
4.设复数z=x+yi,(x,y∈R,y≠0),w=x+$\frac{3x}{{x}^{2}+{y}^{2}}$+(y-$\frac{3y}{{x}^{2}+{y}^{2}}$)i,且2≤w≤4,Rez的取值范围是[1,2].分析 由题意可得x2+y2=3,代入2≤x+$\frac{3x}{{x}^{2}+{y}^{2}}$≤4可得x的不等式,解不等式可得.
解答 解:∵w=x+$\frac{3x}{{x}^{2}+{y}^{2}}$+(y-$\frac{3y}{{x}^{2}+{y}^{2}}$)i,且2≤w≤4,
∴y-$\frac{3y}{{x}^{2}+{y}^{2}}$=0,且2≤x+$\frac{3x}{{x}^{2}+{y}^{2}}$≤4,
结合x,y∈R,y≠0可得x2+y2=3,
∴代入2≤x+$\frac{3x}{{x}^{2}+{y}^{2}}$≤4可得2≤2x≤4,
解得1≤x≤2,即1≤Rez≤2,
故答案为:[1,2]
点评 本题考查复数的代数形式的混合运算,涉及整体法和不等式的性质,属基础题.

练习册系列答案
相关题目
14.已知实数x,y满足不等式组$\left\{\begin{array}{l}x≤1\\ x+y+2≥0\\ kx-y≥0\end{array}\right.$,若目标函数z=2x-y仅在点(1,k)处取得最小值,则实数k的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | [1,+∞) | D. | (1,+∞) |
12.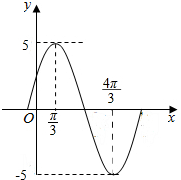 函数f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ),x∈R,其中a,b,ω都为正数,在一个周期内的图象如图,满足f(x)<$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是( )
函数f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ),x∈R,其中a,b,ω都为正数,在一个周期内的图象如图,满足f(x)<$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是( )
 函数f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ),x∈R,其中a,b,ω都为正数,在一个周期内的图象如图,满足f(x)<$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是( )
函数f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ),x∈R,其中a,b,ω都为正数,在一个周期内的图象如图,满足f(x)<$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是( )| A. | (-∞,2kπ),k∈Z | B. | (2kπ-π,2kπ),k∈Z | C. | (2kπ-2π,2kπ),k∈Z | D. | (2kπ-$\frac{4π}{3}$,2kπ),k∈Z |
13.$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,-2),则<$\overrightarrow{a}$,$\overrightarrow{b}$>=( )
| A. | 0° | B. | 60° | C. | 90° | D. | 180° |
14.已知全集U=R,集合M={x|x2-x-6>0},则∁UM=( )
| A. | (-2,3) | B. | ∅ | C. | [-2,3] | D. | R |