题目内容
等差数列{an}的前n项和记为Sn,若a2+a4+a6的值为一确定的常数,则下列各数中也是常数的是( )
| A、S7 |
| B、S8 |
| C、S13 |
| D、S15 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由题意,可先化简a2+a4+a6得出a4是一个常数,再由等差数列的性质得出S7=
(a1+a7)=21a4,即可得出正确选项
| 7 |
| 2 |
解答:
解:由等差数列{an}的性质可得a2+a6=2a4.
∴a2+a4+a6=3a4.
∴S7=
(a1+a7)=21a4是一个常数
故选:A.
∴a2+a4+a6=3a4.
∴S7=
| 7 |
| 2 |
故选:A.
点评:本题考点是等差数列的性质,考察了等差数列的通项公式,等差数列的性质,解题的关键是熟练掌握数列的性质.

练习册系列答案
相关题目
f(x)=
则f[f(
)]=( )
|
| 1 |
| 4 |
| A、9 | ||
B、
| ||
| C、1 | ||
| D、3 |
若球的半径为1,则其体积为( )
| A、π | ||
B、
| ||
C、
| ||
| D、2π |
不等式2x-y-6<0表示的平面区域在直线2x-y-6=0的( )
| A、左上方 | B、右上方 |
| C、左下方 | D、右下方 |
焦点在x轴上的双曲线
-
=1的两条渐近线与抛物线y=x2+1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
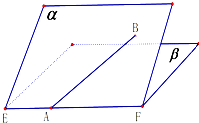 如图,二面角α-EF-β的大小是60°,线段AB?α,A在EF上,AB与β所成的角为30°,则sin∠BAF=
如图,二面角α-EF-β的大小是60°,线段AB?α,A在EF上,AB与β所成的角为30°,则sin∠BAF=