题目内容
定义平面向量之间的一种运算“△”如下：对任意的
=(m，n)，
=(p，q)，令
△
=mq-np，下面说法错误的是 ．
①若
与
共线，则
△
=0
②
△
=
△
③对任意的λ∈R，有（λ
）△
=λ（
△
）
④
△
=0
⑤(
△
)2+(
•
)=|
|2|
|2．
| a |
| b |
| a |
| b |
①若
| a |
| b |
| a |
| b |
②
| a |
| b |
| b |
| a |
③对任意的λ∈R，有（λ
| a |
| b |
| a |
| b |
④
| a |
| a |
⑤(
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：将新定义的问题转化为我们熟知的向量的运算解决．
解答：
解：由题意，①若
与
共线，则mq=np，所以
△
=0成立；
②由新定义
△
=mq-np，
△
=pn-qm=-（np-mq）=-
△
；故②不成立；
③λ
=（λm，λn），（λ
）△
=λmq-λnp，λ（
△
）=λmq-λnp，所以对任意的λ∈R，有（λ
）△
=λ（
△
）成立；
④
△
=mn-nm=0，成立；
⑤（
△
）2+
•
=（mq-np）2+mp+nq，|
|2|
|2=(m2+n2)(p2+q2)≠（mq-np）2+mp+nq，所以⑤不成立；
故答案为：②⑤．
| a |
| b |
| a |
| b |
②由新定义
| a |
| b |
| b |
| a |
| a |
| b |
③λ
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④
| a |
| a |
⑤（
| a |
| b |
| a |
| b |
| a |
| b |
故答案为：②⑤．
点评：本题考查了向量运算的新定义问题，关键是将新定义转化为熟悉的问题解答．
练习册系列答案
相关题目
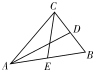如图，在Rt△ABC中，∠C=90°，AC=4，BC=2，D、E分别是BC、AB的中点，P是△ABC（包括边界）内任一点，则| AD |
| EP |
| A、[-7，7] |
| B、[-8，8] |
| C、[-9，9] |
| D、[-10，O] |
已知f（x）=
x3-
x2-2x+1，则该函数的单调递增区间为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、（-∞，-1） |
| B、（2，+∞） |
| C、（-1，2） |
| D、（-∞，-1）和（2，+∞） |
有一个几何体的三视图如下图所示，这个几何体应是一个（ ）
| A、棱锥 | B、圆锥 | C、圆柱 | D、棱柱 |