题目内容
一个边长为2的正方形铁片,铁片的四角截去四个边长都相等的小正方形(如图),然后做成一个底边长为x无盖方盒:①试把方盒的容积V表示为x的函数;②x多大时容积V最大?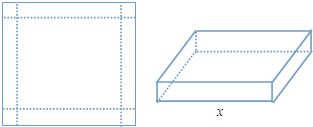

考点:函数解析式的求解及常用方法,棱柱、棱锥、棱台的体积
专题:函数的性质及应用
分析:①由题设知这个无盖方盒的底面是边长为2-2x的正方形,高为x的正四棱柱,由此能把方盒的容积V表示为x的函数.
②由(1)知V=(2-2x)2x,0<x<1,求导数,令V′=0,得x1=
,x2=1(舍).由此得到函数的单调增和单调减区间,能求出这个方盒容积的最大值和取到最大值时x的值.
②由(1)知V=(2-2x)2x,0<x<1,求导数,令V′=0,得x1=
| 1 |
| 3 |
解答:
解:由于是在边长为2的正方形铁片的四角各截去一个边长为x的小正方形做成一个无盖方盒,
所以无盖方盒的底面为正方形,且边长为2-2x,高为x,
(1)所以,无盖方盒的容积V=(2-2x)2x,0<x<1,
(2)∵V=(2-2x)2x,
∴V′=12x2-16x+4;
令:V′(x)=0,即12x2-16x+4=0,
∴x=
或x=1,(0<x<1),
∴x=
;
当x∈(0,
)时,V′(x)>0;
当x∈(
,1)时,V′(x)<0.
因此,x=
是函数f(x)的极大值点,也就是最大值点,且最大值为
.
所以无盖方盒的底面为正方形,且边长为2-2x,高为x,
(1)所以,无盖方盒的容积V=(2-2x)2x,0<x<1,
(2)∵V=(2-2x)2x,
∴V′=12x2-16x+4;
令:V′(x)=0,即12x2-16x+4=0,
∴x=
| 1 |
| 3 |
∴x=
| 1 |
| 3 |
当x∈(0,
| 1 |
| 3 |
当x∈(
| 1 |
| 3 |
因此,x=
| 1 |
| 3 |
| 16 |
| 27 |
点评:本题考查方盒容积的求法,考查利用导数求方盒容积的最大值,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目