题目内容
分别求圆x2+y2=1过下列点的切线方程:
(1)(-1,0);
(2)(-1,2).
(1)(-1,0);
(2)(-1,2).
考点:圆的切线方程
专题:直线与圆
分析:(1)由于点(-1,0)正好是单位圆x2+y2=1与x轴的交点,可得圆的切线方程.
(2)当切线的斜率不存在时,求得切线方程;当切线斜率存在时,用点斜式设切线方程,由圆心(0,0)到切线的距离等于半径求得斜率k的值,可得此时切线的方程.
(2)当切线的斜率不存在时,求得切线方程;当切线斜率存在时,用点斜式设切线方程,由圆心(0,0)到切线的距离等于半径求得斜率k的值,可得此时切线的方程.
解答:
解:(1)由于点(-1,0)正好是单位圆x2+y2=1与x轴的交点,故圆的切线方程为x=1.
(2)当切线的斜率不存在时,切线方程为x=-1,
当切线斜率存在时,设切线方程为y-2=k(x+1),即 kx-y+2+k=0,
由圆心(0,0)到切线的距离等于半径可得
=1,求得k=-
,故此时切线的方程为3x+4y-5=0.
综上可得,所求的圆的切线方程为 x=-1,或 3x+4y-5=0.
(2)当切线的斜率不存在时,切线方程为x=-1,
当切线斜率存在时,设切线方程为y-2=k(x+1),即 kx-y+2+k=0,
由圆心(0,0)到切线的距离等于半径可得
| |0-0+2+k| | ||
|
| 3 |
| 4 |
综上可得,所求的圆的切线方程为 x=-1,或 3x+4y-5=0.
点评:本题主要考查求圆的切线方程,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目


 如图,已知P是正方形ABCD平面外一点,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
如图,已知P是正方形ABCD平面外一点,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
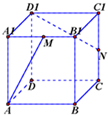 如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角
如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角