题目内容
直线l过点 （-3，-2）且在两坐标轴上的截距相等，求这条直线的方程．
考点：直线的截距式方程
专题：直线与圆
分析：讨论直线l在两坐标轴上的截距为0以及不等于0时，设出直线方程，求出对应的直线方程即可．
解答：
解：当直线l在两坐标轴上的截距为0时，设直线方程为y=kx，
∵直线l过点（-3，-2），
∴-3k=-2，
解得k=
，
直线方程为：y=
x，
即2x-3y=0；
当直线l在两坐标轴上的截距不为0时，设直线方程为x+y=a，
∵直线l过点（-3，-2），
∴-3+（-2）=a，
解得a=-5，
直线方程为x+y=-5，
即x+y+5=0；
∴直线方程为2x-3y=0或x+y+5=0．
∵直线l过点（-3，-2），
∴-3k=-2，
解得k=
| 2 |
| 3 |
直线方程为：y=
| 2 |
| 3 |
即2x-3y=0；
当直线l在两坐标轴上的截距不为0时，设直线方程为x+y=a，
∵直线l过点（-3，-2），
∴-3+（-2）=a，
解得a=-5，
直线方程为x+y=-5，
即x+y+5=0；
∴直线方程为2x-3y=0或x+y+5=0．
点评：本题考查了用分类讨论的方法求直线方程的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
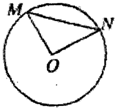如图，M是半径R的圆周上一个定点，在圆周上等可能的任取一点N，连接MN，则弦MN的长度超过| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示，为测一建筑物的高度，在地面上选取A，B两点，从A，B两点分别测得建筑物顶端的仰角为30°，45°，且A，B两点间的距离为60m，则该建筑物的高度为（ ）A、（30+30
| ||
B、（30+15
| ||
C、（15+30
| ||
D、（15+15
|
下列对二次函数y=-x2+1的描述错误的是（ ）
| A、开口向下 |
| B、函数的图象关于y轴对称 |
| C、增区间为（-∞，0] |
| D、有最小值，无最大值 |