题目内容
5.已知等比数列{an}中,a1+a2+a3+a4+a5=31,a2+a3+a4+a5+a6=62,则通项an等于( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
分析 将已知两式相除即可求得q=2,然后根据等比数列的通项公式求得首项.
解答 解:设等比数列{an}的公比为q,
∵a1+a2+a3+a4+a5=31,a2+a3+a4+a5+a6=62,
∴q=$\frac{{a}_{2}+{a}_{3}+{a}_{4}+{a}_{5}+{a}_{6}}{{a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+{a}_{5}}$=$\frac{62}{31}$=2,
∴a1(1+q+q2+q3+q4)=31,
则a1=31,
故an=2n-1.
故选:A.
点评 本题考查了等比数列的性质,等比数列的定义,考查计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知某几何体的三视图如图所示,则此几何体的体积是( )
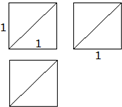

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
17.已知正方体ABCD-A1B1C1D1棱长为1,E、F为线段B1D1的两个动点,且EF=$\frac{\sqrt{2}}{2}$,给出下列四个命题:
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个. |
14.曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1(0<k<9)的关系是( )
| A. | 有相等的焦距,相同的焦点 | B. | 有不同的焦距,不同的焦点 | ||
| C. | 有相等的焦距,不同的焦点 | D. | 以上都不对 |
 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ,集合
,集合 ,则( )
,则( ) B.
B.
 D.
D.
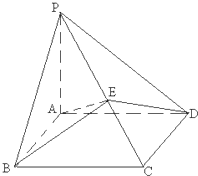 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.