题目内容
1.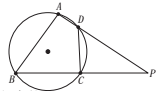 如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P.
如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P.(1)求证:$\frac{BC}{BP}$=$\frac{DC}{DP}$;
(2)求证:∠BDC+$\frac{1}{2}∠PDC={90°}$.
分析 (1)利用“两角法”推知△ABP∽△CDP,在根据该相似三角形的对应边成比例和已知条件AB=BC证得结论;
(2)连接BD,AC,根据圆周角定理和等腰三角形的性质推知∠BDC=∠BDA,所以∠ADC=2∠BDC.根据邻补角的定义推知∠PDC+∠ADC=180°,易证$∠BDC+\frac{1}{2}∠PDC={90°}$.
解答  证明:(1)因为∠PDC=∠PBA,∠APB=∠CPD,
证明:(1)因为∠PDC=∠PBA,∠APB=∠CPD,
所以△ABP∽△CDP,
所以$\frac{AB}{CD}=\frac{BP}{DP}$.
又AB=BC,
所以$\frac{BC}{BP}=\frac{DC}{DP}$.
(2)连接BD,AC,
因为AB=BC,
所以∠BAC=∠BCA,
又∠BAC=∠BDC,∠BCA=∠BDA,
所以∠BDC=∠BDA,
所以∠ADC=2∠BDC.
因为∠PDC+∠ADC=180°,
所以$∠BDC+\frac{1}{2}∠PDC={90°}$.
点评 本题考查了相似三角形的判定与性质,圆周角定理以及等腰三角形的判定与性质.考查学生们的分析能力,属于基础题型.

练习册系列答案
相关题目
14.设抛物线y2=8x的焦点为F,P是抛物线上一点,若直线PF的倾斜角为120°,则|PF|=( )
| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{8}{3}$或8 | D. | 3或8 |
13.已知某几何体的三视图如图所示,则此几何体的体积是( )
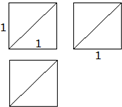

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
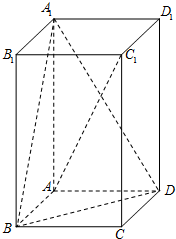 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h. 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.