题目内容
11.已知直线的方程是$\sqrt{3}x-y+1=0$,则直线的倾斜角是( )| A. | 120° | B. | 150° | C. | 30° | D. | 60° |
分析 根据题意,设直线的倾斜角为θ,结合直线的方程可得其斜率k=$\sqrt{3}$,由直线的斜率为倾斜角的关系可得tanθ=$\sqrt{3}$,解可得θ的值,即可得答案.
解答 解:根据题意,设直线的倾斜角为θ,(0°≤θ<180°)
直线的方程是$\sqrt{3}x-y+1=0$,变形可得y=$\sqrt{3}$x+1,
其斜率k=$\sqrt{3}$,
则有tanθ=$\sqrt{3}$,
直线的倾斜角θ=60°;
故选:D.
点评 本题考查直线的倾斜角计算,注意要先求出直线的斜率.

练习册系列答案
相关题目
19.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-4y+3≥0}\\{x+y≥0}\\{x≥1}\end{array}\right.$,目标函数z=2x+y,则( )
| A. | z的最小值为3,z无最大值 | B. | z的最小值为1,最大值为3 | ||
| C. | z的最小值为3,z无最小值 | D. | z的最小值为1,z无最大值 |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$与抛物线y2=4x的交点为A,B,且直线AB过双曲线与抛物线的公共焦点F,则双曲线的实轴长为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 2$\sqrt{2}$-2 |
3.某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个周)和市场占有率(y%)的几组相关数据如表:
(Ⅰ)根据表中的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$;
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个周,该款旗舰机型市场占有率能超过0.40%(最后结果精确到整数).
参考公式:$\widehat{b}=\frac{{{\sum_{i=1}^{n}x}_{i}y}_{y}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\hat a=\bar y-\hat b\bar x$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个周,该款旗舰机型市场占有率能超过0.40%(最后结果精确到整数).
参考公式:$\widehat{b}=\frac{{{\sum_{i=1}^{n}x}_{i}y}_{y}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\hat a=\bar y-\hat b\bar x$.
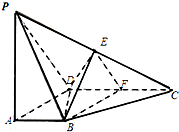 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.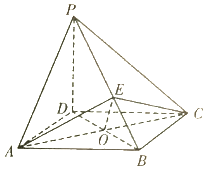 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点.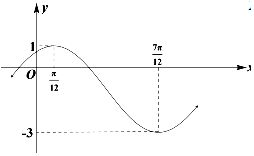 已知函数$f(x)=Asin(wx+φ)+B(A>0,w>0,|φ|<\frac{π}{2})$的 部分图象如图所示:
已知函数$f(x)=Asin(wx+φ)+B(A>0,w>0,|φ|<\frac{π}{2})$的 部分图象如图所示: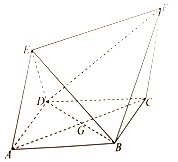 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.