题目内容
若关于x的方程cosx-1+m=0在区间[0,
]有解,则实数m的取值范围为 .
| 2π |
| 3 |
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:由题意可得m=1-cosx,x∈[0,
],再根据余弦函数的定义域和值域求得实数m的取值范围.
| 2π |
| 3 |
解答:
解:由题意可得m=1-cosx,x∈[0,
],
由x∈[0,
],可得cosx∈[-
,1],故m=1-cosx∈[0,
],
故答案为:[0,
].
| 2π |
| 3 |
由x∈[0,
| 2π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:[0,
| 3 |
| 2 |
点评:本题主要考查余弦函数的定义域和值域,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
若偶函数f(x)在(-∞,0]上是增函数,则下列关系式中成立的是( )
A、f(-
| ||
B、f(2)<f(-1)<f(-
| ||
C、f(2)<f(-
| ||
D、f(-1)<f(-
|
已知a是实数,则“0<a<1”是“方程x2+y2-2ax+2a2-1=0表示圆”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集U={1,2,3,4,5,6},集合A={1,3,5},B={1,2},∁U(A∪B)等于(
| A、{4} | B、{6} |
| C、{4,6} | D、∅ |
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(23)+f(-14)=( )
| A、-1 | B、1 | C、-2 | D、2 |
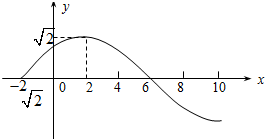 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<