题目内容
16.已知△ABC的三个顶点的坐标分别为A(3,0),B(4,6),C(0,8).(1)求BC边上的高所在直线l的方程;
(2)求△ABC的面积.
分析 (1)求出BC的斜率,带入点斜式方程即可;(2)求出AC的长,根据AC的方程,求出点B到直线AC的距离,从而求出三角形ABC的面积即可.
解答 解:(1)因为点B(4,6),C(0,8),则kBC=$\frac{8-6}{0-4}$=-$\frac{1}{2}$,
因为l⊥BC,则l的斜率为2.
又直线l过点A,所以直线l的方程为y=2(x-3),即2x-y-6=0.
(2)因为点A(3,0),C(0,8),则|AC|=$\sqrt{9+64}$=$\sqrt{73}$,
又直线AC的方程为$\frac{x}{3}$+$\frac{y}{8}$=1,即8x+3y-24=0,
则点B到直线AC的距离d=$\frac{32+18-24}{\sqrt{64+9}}$=$\frac{26}{\sqrt{73}}$,
所以△ABC的面积S=$\frac{1}{2}$|AC|×d=13.
点评 本题考查了求直线方程问题,考查考查点到直线的距离公式,是一道中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
6.若角θ是第四象限的角,则角${-^{\;}}\frac{θ}{2}$是( )
| A. | 第一、三象限角 | B. | 第二、四象限角 | C. | 第二、三象限角 | D. | 第一、四象限角 |
8.已知向量$\vec n=(2,0,1)$为平面α的一个法向量,点A(-1,2,1)在α内,则P(1,2,-2)到平面α的距离为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
6.在各项为正实数的等差数列{an}中,其前2016项的和S2016=1008,则$\frac{1}{{{a_{1001}}}}+\frac{1}{{{a_{1016}}}}$的最小值为( )
| A. | 6 | B. | 4 | C. | $\frac{1}{84}$ | D. | $\frac{1}{251}$ |
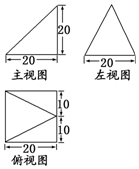 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.