题目内容
8.已知向量$\vec n=(2,0,1)$为平面α的一个法向量,点A(-1,2,1)在α内,则P(1,2,-2)到平面α的距离为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
分析 点P(1,2,-2)到平面α的距离d=$\frac{|\overrightarrow{AP}•\overrightarrow{n}|}{|\overrightarrow{n}|}$,由此能求出结果.
解答 解:∵平面α的一个法向量为$\overrightarrow{n}$=(2,0,1),
点A(-1,2,1)在平面α内,点P(1,2,-2),
∴$\overrightarrow{AP}$=(2,0,-3),
∴点P(1,2,-2)到平面α的距离d═$\frac{|\overrightarrow{AP}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\sqrt{5}$.
故选:B.
点评 本题考查点到平面的距离的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
19.下列有关命题的说法错误的为( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “|x|<2”是“x2-x-6<0”的充分不必要条件 | |
| C. | 命题“存在∈R,使得x2+x+1<0”的否定是“对任意x∈R,均有x2+x+1≥0” | |
| D. | 若p∧q为假命题,则p,q均为假 |
13.取一根长度为4m的绳子,拉直后在任意位置剪断,则剪得的两段长度都不小于1.5m的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
20.设a=log43,b=log34,c=log53,则( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
17.过点M(1,1)的直线与椭圆$\frac{x^2}{12}+\frac{y^2}{9}=1$交于A,B两点,且点M平分弦AB,则直线AB方程为( )
| A. | 4x+3y-7=0 | B. | 3x+4y-7=0 | C. | 3x-4y+1=0 | D. | 4x-3y-1=0 |
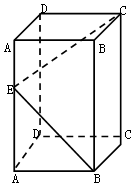 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )