题目内容
已知a=lg（1+
），b=lg（1+
），使用含a、b的式子表示lg1.4．
| 1 |
| 7 |
| 1 |
| 49 |
考点：对数的运算性质
专题：函数的性质及应用
分析：由已知得a=3lg2-lg7，b=2-lg2-2lg7，从而lg2=
（2a-b+2），lg7=
（6-a-3b），由此能使用含a、b的式子表示lg1.4．
| 1 |
| 7 |
| 1 |
| 7 |
解答：
解：a=lg（1+
）=lg
=lg8-lg7=3lg2-lg7，
b=lg（1+
）=lg
=lg50-lg49
=lg
-lg49=lg100-lg2-2lg7=2-lg2-2lg7
因为3lg2-lg7=a，2-lg2-2lg7=b
两式联立得lg2=
（2a-b+2），lg7=
（6-a-3b），
lg1.4=lg
=lg14-1=lg2+lg7-1
=
（2a-b+2）+
（6-a-3b）-1=
．
| 1 |
| 7 |
| 8 |
| 7 |
b=lg（1+
| 1 |
| 49 |
| 50 |
| 49 |
=lg
| 100 |
| 2 |
因为3lg2-lg7=a，2-lg2-2lg7=b
两式联立得lg2=
| 1 |
| 7 |
| 1 |
| 7 |
lg1.4=lg
| 14 |
| 10 |
=
| 1 |
| 7 |
| 1 |
| 7 |
| a-4b+1 |
| 7 |
点评：本题考查对数的性质的应用，是中档题，解题时要认真审题，注意对数性质的合理运用．
练习册系列答案
相关题目
数列{-2n2+29n+3}中最大项是（ ）
| A、107 | ||
| B、108 | ||
C、108
| ||
| D、109 |
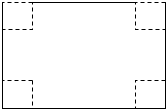如图，一矩形铁皮的长为8cm，宽为5cm，在四个角上截去四个相同的小正方形，制成一个无盖的小盒子，问小正方形的边长为