题目内容
19.已知集合A={x|log2x≤1},B={x|$\frac{1}{x}$>1},则A∩(∁RB)=( )| A. | (-∞,2] | B. | (0,1] | C. | [1,2] | D. | (2,+∞) |
分析 求函数定义域求出集合A,解不等式求出集合B,
根据补集与交集的定义写出A∩(∁RB).
解答 解:集合A={x|log2x≤1}={x|0<x≤2},
B={x|$\frac{1}{x}$>1}={x|$\frac{1}{x}$-1>0}={x|0<x<1},
∴∁RB={x|x≤0或x≥1},
∴A∩(∁RB)={x|1≤x≤2}=[1,2].
故选:C.
点评 本题考查了求函数定义域和解不等式的应用问题,也考查了补集与交集的运算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.化简y=$\frac{2sin2α}{1+cos2α}$( )
| A. | tanα | B. | tan2α | C. | 2tanα | D. | 2tan2α |
14.已知集合A={x|x2+4≤5x,x∈R},B={y|y>2},则A∩B=( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (2,4] | D. | [2,4] |
4.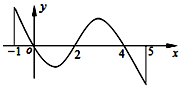 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
下列关于函数f(x)的命题:
①函数f(x)的极大值点有2个;
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中是真命题的是①②.(填写序号)
 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数f(x)的极大值点有2个;
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中是真命题的是①②.(填写序号)
11.下列关于回归分析与独立性检验的说法正确的是( )
| A. | 回归分析和独立性检验没有什么区别 | |
| B. | 回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系 | |
| C. | 回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验 | |
| D. | 独立性检验可以100%确定两个变量之间是否具有某种关系 |
12.已知△ABC中,AD是BC边上的中线,且cos∠BAC=$\frac{4}{5}$,cosC=$\frac{5}{13}$,BC=26.
(1)求AB的长;
(2)求cosB;
(3)求AD的长.
(1)求AB的长;
(2)求cosB;
(3)求AD的长.
13.直线ax+2y+1=0和直线3x+(a-1)y+1=0平行,则a=( )
| A. | -2 | B. | 2或-3 | C. | 3 | D. | -2或3 |
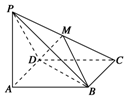 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).