题目内容
判断下列函数的奇偶性
(1)f(x)=
;
(2)f(x)=0,x∈[-6,-2]∪[2,6].
(1)f(x)=
| ||
| |x+2|-2 |
(2)f(x)=0,x∈[-6,-2]∪[2,6].
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:(1)由1-x2≥0且|x+2|-2≠0,求出定义域,化简函数式,计算f(-x),与f(x)比较,即可判断其偶性;
(2)考虑定义域关于原点对称,再由定义即可判断其偶性.
(2)考虑定义域关于原点对称,再由定义即可判断其偶性.
解答:
解:(1)由1-x2≥0且|x+2|-2≠0,解得-1≤x≤1且x≠0,
则定义域关于原点对称,
则f(x)=
,f(-x)=
=-f(x),
故f(x)为奇函数;
(2)定义域[-6,-2]∪[2,6]关于原点对称,
f(-x)=f(x)=0,且f(-x)=-f(x),
则f(x)既是奇函数,也为偶函数.
则定义域关于原点对称,
则f(x)=
| ||
| x |
| ||
| -x |
故f(x)为奇函数;
(2)定义域[-6,-2]∪[2,6]关于原点对称,
f(-x)=f(x)=0,且f(-x)=-f(x),
则f(x)既是奇函数,也为偶函数.
点评:本题考查函数的奇偶性的判断,注意定义域是否关于原点对称,化简函数式,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
过点(1,3)且斜率为3的直线方程为( )
| A、y-3=3(x-1) |
| B、y-3=3(x+1) |
| C、y+3=3(x-1) |
| D、y+3=3(x+1) |
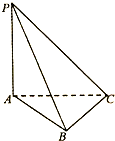 如图,在三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△PAC是直角三角形,∠PAC=90°,∠ACP=30°,平面PAC⊥平面ABC.
如图,在三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△PAC是直角三角形,∠PAC=90°,∠ACP=30°,平面PAC⊥平面ABC.